

É um poliedro convexo cuja base é um polígono convexo e as demais faces são triângulos que têm um vértice comum.
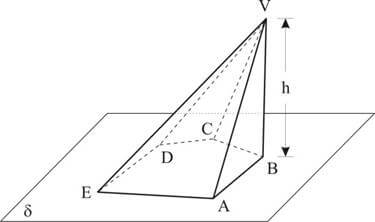
Elementos:
A pirâmide recebe o nome de acordo com o número de lados do polígono da base.

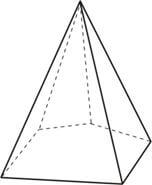
Secção transversal é a intersecção da pirâmide com um plano paralelo à base.
Propriedades:
Pirâmide regular é toda pirâmide cuja base é um polígono regular. As faces laterais são triângulos isósceles congruentes entre si.
Desta forma, uma pirâmide regular quadrangular, possui como base um quadrado, uma pirâmide regular pentagonal, possui base pentagonal, e assim por diante.
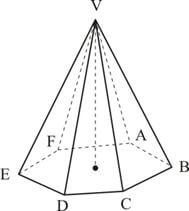
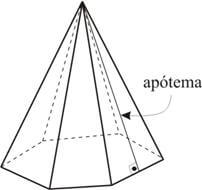
Apótema de uma pirâmide regular é o segmento cujas extremidades são o vértice e o ponto médio de uma aresta da base.
Tetraedro é uma pirâmide triangular.
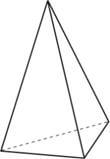
Tetraedro regular é um tetraedro que tem as seis arestas congruentes entre si.
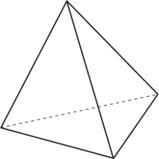
As quatro faces são triângulos equiláteros congruentes entre si.
A área lateral de uma pirâmide é a área de sua superfície lateral.
A área total de uma pirâmide é a soma das áreas de todas as faces que a limitam: a base e os triângulos que compõe a lateral da pirâmide.
O volume de uma pirâmide é dado por
V = \( \dfrac{1}{3} \) ∙ S\(_B\) ∙ H
Determine o volume de uma pirâmide quadrangular regular cuja aresta da base mede 6 cm e altura mede 4 cm.
Solução
V = \( \dfrac{1}{3} \) ∙ S\(_B\) ∙ h
V = \( \dfrac{1}{3} \) ∙ 6² ∙ 4
V = 48 cm³
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.