

O limite é muito utilizado em engenharias e quando se necessita saber tendência de alguma situação.
Exemplos
Seja A um subconjunto não vazio dos \(\mathbb{R}\).
Um número a diz-se ponto de acumulação de A se e só se em qualquer vizinhança em a exista pelo menos um elemento de A e diferente de a.
Um número a pertencente a A é um ponto isolado de A se não é ponto de acumulação.
Exemplo:
Sendo A = [-2, 3[ ∪ {5}, tem-se que:
O conjunto dos pontos de acumulação de A é [- 2, 3] e 5 é um ponto isolado de A.
No conjunto B = {0} ∪ ]2, 10], 0 ______ ponto de acumulação de B.
Um elemento de um subconjunto dos números reais
Vamos aprender agora o limite de uma função num ponto (limites laterais).
Considere a função real de variável real f definida por:
f(x) = \(\left \{ \begin{matrix} x + 1, x \geq 1 \\ -x + 2, x < 1 \end{matrix} \right.\)
cujo o gráfico é:
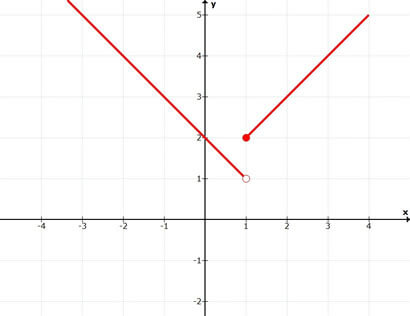
Note que:
Para entender o comportamento da função quando x se aproxima de 2 podemos elaborar tabelas.
| x | f(x) |
|---|---|
| 3 | 4 |
| 2,5 | 3,5 |
| \(\dfrac{7}{3}\) | \(\dfrac{10}{3}\) |
| ... | ... |
| (2\(^+\)) | 3 |
| x | f(x) |
|---|---|
| 1 | 2 |
| 1,5 | 2,5 |
| \(\dfrac{5}{3}\) | \(\dfrac{8}{3}\) |
| ... | ... |
| (2\(^-\)) | 3 |
A primeira tabela mostra que a medida que x se aproxima de 2 por valores superiores a 2 (ou seja, se aproxima de 2 pela direita), os valores correspondentes da função se aproximam de 3.
Em outras palavras:
Se x → \(2^+\), então f(x) → 3
se x tende a 2 pela direita, então f(x) tende a 3
Em linguagem matemática, escrevemos:
\(lim_{x \to 2^+} f(x) = 3\)
limite de f(x) quando x tende a 2 pela direita é igual a 3
De modo análogo, a segunda tabela mostra que a medida que x se aproxima de 2 por valores inferiores a 2 (ou seja, se aproxima de 2 pela esquerda), os valores correspondentes da função se aproximam de 3.
Em outras palavras:
Se x → \(2^-\), então f(x) → 3
se x tende a 2 pela esquerda, então f(x) tende a 3
Portanto:
\(lim_{x \to 2^-} f(x) = 3\)
limite de f(x) quando x tende a 2 pela esquerda é igual a 3
Notou que o limite de f(x) é 3 em ambos os lados?
Como esses limites, chamados de laterais, existem e são iguais, dizemos que:
\(lim_{x \to 2} f(x)= 3\)
limite de f(x) quando x tende a 2 é igual a 3
E qual é o comportamento da função quando x se aproxima de 1? Vamos ver...
| x | f(x) |
|---|---|
| 2 | 3 |
| 1,5 | 2,5 |
| 1,2 | 2,2 |
| ... | ... |
| (1\(^+\)) | 2 |
| x | f(x) |
|---|---|
| 0 | 2 |
| 0,5 | 1,5 |
| 0,7 | 1,3 |
| ... | ... |
| (1\(^-\)) | 1 |
Pela primeira tabela, a medida que x se aproxima de 1 por valores superiores a 1, a função tende a 2.
\(lim_{x \to 1^+} f(x) = 2\)
limite de f(x) quando x tende a 1 pela direita é 2
Pela segunda tabela, a medida que x se aproxima de 1 por valores inferiores a 1, a função tende para 1.
\(lim_{x \to 1^-} f(x) = 1\)
limite de f(x) quando x tende a 1 pela esquerda é igual a 1
Os limites laterais existem mas são diferentes. Desta forma, não existe \(lim_{x \to 1} f(x)\).
Considere as funções f(x), h(x) e g(x):
Graficamente, temos:
a) 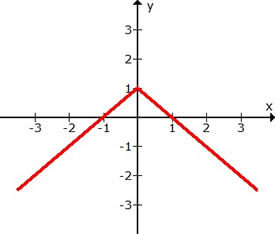
b) 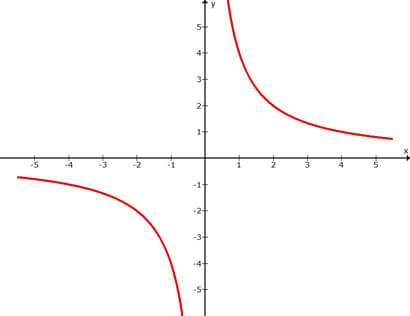
c) 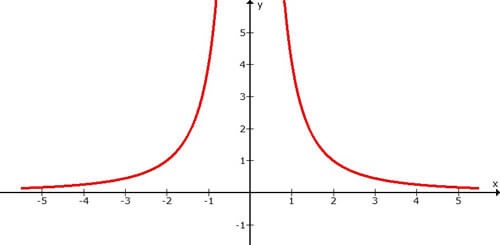
Em (a), temos que o limite de f(x) quando x tende a 0 é 1.
\(lim_{x \to 0}\) f(x) = 1
Em (b), os limites laterais são diferentes. Quando x tende a 0:
Logo, não existe \(lim_{x \to 0}\) h(x).
O limite de uma função num ponto, se existir, pode ser um número real, mas também pode ser igual a +\(\infty\) ou -\(\infty\).
Em (c), temos que o limite de g(x) quando x tende a 0 é +\(\infty\).
\(lim_{x \to 0}\) g(x) = +\(\infty\)
Analisamos os limites das funções quando x tende a 0, mas podemos, também, calcular o limite de uma função quando x → +\(\infty\) ou x → -\(\infty\).
Estudar o comportamento de uma função quando x → +\(\infty\) (ou x → -\(\infty\)) só é possível quando o domínio não for limitado superiormente (ou inferiormente).
Nos gráficos acima temos:
a) \(lim_{x \to \pm \infty}\) f(x) = -\(\infty\)
b) \(lim_{x \to \pm \infty}\) h(x) = 0
c) \(lim_{x \to \pm \infty}\) g(x) = 0
Para obter o limite de uma função, quando x tende para um número real a, basta substituir x por a.
Exemplo:
\(lim_{x \to 3} x^2 - 2x^3 + 1\)
Substituindo x por 3, tem-se:
3² - 2 (3)\(^3\) + 1 = 9 - (2 ∙ 27) + 1 = -44
Logo:
\(lim_{x \to 3} (x^2 - 2x^3 + 1)\) = -44
\(lim_{x \to -2} \dfrac{3x - 2}{x^3 - x}\)
Substituindo x por -2, tem-se:
\(\dfrac{3 (-2) - 2}{(-2)^3 - (-2)} = \dfrac{-8}{-6} = \dfrac{4}{3}\)
Portanto, \(lim_{x \to 2} \dfrac{3x-2}{x^3 - x} = \dfrac{4}{3}\)
\(lim_{x \to 1} \dfrac{5x + 2}{x - 1}\)
Substituindo x por 1, tem-se:
\(lim_{x \to 1} \dfrac{5x + 2}{x - 1} = lim_{x \to 1} \dfrac{5 (1) + 2}{1 - 1} = \dfrac{7}{0}\)
Esse limite não será um número real.
Observação:
Para saber se existe limite é necessário calcular os limites laterais.
\(lim_{x \to 1^+} \dfrac{5x + 2}{x - 1} = lim_{x \to 1} \dfrac{5 (1) + 2}{1 - 1} = \dfrac{7}{0^+}\) = +\(\infty\)
Quando x tende a 1 pela direita, o denominador na fração tende a zero pela direita (valor positivo se aproximando do zero). Logo, 7 dividido por um número positivo se aproximando do zero é igual a um número infinito positivo (+\(\infty\)).
\(lim_{x \to 1^-} \dfrac{5x + 2}{x - 1} = lim_{x \to 1} \dfrac{5 (1) + 2}{1 - 1} = \dfrac{7}{0^-}\) = -\(\infty\)
Quando x tende a 1 pela esquerda, o denominador na fração tende a zero pela esquerda (valor negativo se aproximando do zero). Logo, 7 dividido por um número negativo se aproximando do zero é igual a um número infinito negativo (-\(\infty\)).
Note que os limites laterais são diferentes. Logo não existe limite.
Determine os seguintes limites
Solução
a) \(lim_{x \to 1} (4x^2 - 7x + 5)\) = 4(1)² - 7(1) + 5 = 4 - 7 + 5 = 2
b) \(lim_{x \to -3} \dfrac{x^2 + 2x - 3}{5 - 3x}\) = \(\dfrac{(-3)^2 + 2(-3) - 3}{5 - 3(-3)}\) = \(\dfrac{9 - 6 - 3}{5 + 9}\) = \(\dfrac{0}{14}\) = 0
c) \(lim_{x \to 2} \left( \dfrac{3x^2 - 2x - 5}{-x^2 + 3x + 4} \right)^3\) = \(\left( \dfrac{3(2)^2 - 2(2) - 5}{-(2)^2 + 3(2) + 4} \right)^3\) = \(\left( \dfrac{12 - 4 - 5}{-4 + 6 + 4} \right)^3\) = \(\left( \dfrac{3}{6} \right)^3\) = \(\left( \dfrac{1}{2} \right)^3\) = 1/8
d) \(lim_{x \to -1} \sqrt{ \dfrac{2x^2 + 3x - 3}{5x - 4} }\) = \(\sqrt{ \dfrac{2(-1)^2 + 3(-1) - 3}{5(-1) - 4} }\) = \(\sqrt{ \dfrac{2 - 3 - 3}{-5 - 4} }\) = \(\sqrt{ \dfrac{-4}{-9} }\) = 2/3
e) \(lim_{x \to 2} \dfrac{\sqrt{2x^2 + 3x + 2}}{6 - 4x}\) = \(\dfrac{\sqrt{2(2)^2 + 3(2) + 2}}{6 - 4(2)}\) = \(\dfrac{\sqrt{8 + 6 + 2}}{6 - 8}\) = \(\dfrac{\sqrt{16}}{-2}\) = \(\dfrac{4}{-2}\) = -2
Calcule os seguintes limites
Solução
a) \(lim_{x \to +\infty} (2x + 3)\) = 2(∞) + 3 = ∞
b) \(lim_{x \to -\infty} (4 - 5x)\) = 4 - 5(-∞) = 4 + ∞ = ∞
c) \(lim_{x \to -\infty} (3x^3 - 4)\) = 3(-∞)\(^3\) - 4 = 3(-∞) - 4 = -∞ - 4 = -∞
No cálculo de limites, podemos nos deparar com respostas como \(\dfrac{0}{0}\), \(\dfrac{\infty}{\infty}\), \(\infty\) - \(\infty\), 0 ∙ \(\infty\), 0\(^0\), 0\(^\infty\), 1\(^\infty\), etc.
Estes são símbolos de indeterminação, logo teremos que encontrar outra forma para resolver o limite.
1º Caso: x → a
a) \(lim_{x \to 2} \dfrac{x^2 + x - 6}{x^2 - 3x + 2}\)
Substituindo x por 2, tem-se
\(lim_{x \to 2} \dfrac{(2)^2 + (2) - 6}{(2)^2 - 3(2) + 2}\) = \(\dfrac{0}{0}\) (?)
Repare que 2 é a raiz das duas equações, o que faz chegar na indeterminação do tipo \(\dfrac{0}{0}\).
Assim para resolver esse limite podemos decompor em fatores ambos os termos da fração para simplificá-los e assim resolver o limite.
1ª equação: x² + x - 6
Como vimos a raiz dessa equação é o 2. Por Briot-Ruffini, vem:
| 1 | 1 | -6 | |
| 2 | 2 | 6 | |
| 1 | 3 | 0 |
x² + x - 6 = (x - 2)(x + 3)
2ª equação: x² - 3x + 2
Como vimos a raiz dessa equação é o 2. Por Briot-Ruffini, vem:
| 1 | -3 | 2 | |
| 2 | 2 | -2 | |
| 1 | -1 | 0 |
x² - 3x + 2 = (x - 2)(x - 1)
Então tem-se:
\(lim_{x \to 2} \dfrac{x^2 + x - 6}{x^2 - 3x + 2}\) = \(lim_{x \to 2} \dfrac{(x - 2)(x + 3)}{(x - 2)(x - 1)}\) = \(lim_{x \to 2} \dfrac{x + 3}{x - 1}\)
Substituindo x por 2:
\(lim_{x \to 2} \dfrac{2 + 3}{2 - 1}\) = \(\dfrac{5}{1}\) = 5
Logo \(lim_{x \to 2} \dfrac{x^2 + x - 6}{x^2 - 3x + 2}\) = 5
b) \(lim_{x \to 4} \dfrac{x - 4}{\sqrt{x} - 2}\)
Substituindo x por 4, tem-se:
\(\dfrac{x - 4}{\sqrt{x} - 2}\) = \(\dfrac{4 - 4}{\sqrt{4} - 2}\) = \(\dfrac{0}{0}\) (?)
Neste caso devemos multiplicar e dividir pelo conjugado do denominador (neste caso, \(\sqrt{4}\) + 2), já que (a - b)(a + b) = a² - b².
\(\dfrac{x - 4}{\sqrt{x} - 2}\) = \(\dfrac{(x - 4)(\sqrt{x} + 2)}{(\sqrt{x} - 2)(\sqrt{x} + 2)}\) = \(\dfrac{(x - 4)(\sqrt{x} + 2)}{\sqrt{x}^2 - 2^2}\) = \(\sqrt{x}\) + 2
\(lim_{x \to 4} \dfrac{x - 4}{\sqrt{x} - 2}\) = \(lim_{x \to 4} \sqrt{x} + 2\)
Substituindo x por 4, tem-se:
\(lim_{x \to 4} \sqrt{x} + 2\) = \(\sqrt{4}\) + 2 = 2 + 2 = 4
Portanto:
\(\dfrac{x - 4}{\sqrt{x} - 2}\) = 4
2º Caso: x → ±\(\infty\)
a) \(lim_{x \to +\infty} \dfrac{3x^2 + 2x}{5x^2 - 1}\)
Substituindo x por +\(\infty\), tem-se:
\(\dfrac{3x^2 + 2x}{5x^2 - 1}\) = \(\dfrac{3(\infty)^2 + 2(\infty)}{5(\infty)^2 - 1}\) = \(\dfrac{\infty + \infty}{\infty - 1}\) = \(\dfrac{\infty}{\infty}\) (?)
Para resolver este limite temos que colocar em evidência no numerador e denominador, a potência de base x com maior expoente.
\(\dfrac{3x^2 + 2x}{5x^2 - 1}\) = \(\dfrac{x^2 \left( 3 + \dfrac{2}{x}\right)}{x^2 \left( 5 - \dfrac{1}{x^2} \right)}\) = \(\dfrac{3 + \dfrac{2}{x}}{5 - \dfrac{1}{x^2}}\)
Substituindo x por +\(\infty\), tem-se:
\(\dfrac{3 + \dfrac{2}{x}}{5 - \dfrac{1}{x^2}}\) = \(\dfrac{3 + \dfrac{2}{\infty}}{5 - \dfrac{1}{\infty^2}}\) = \(\dfrac{3 + 0}{5 - 0}\) = \(\dfrac{3}{5}\)
Logo:
\(lim_{x \to +\infty} \dfrac{3x^2 + 2x}{5x^2 - 1}\) = \(\dfrac{3}{5}\)
Determine \(lim_{x \to 1} \dfrac{x^2 - 1}{x - 1}\)
Solução
\(lim_{x \to 1} \dfrac{x^2 - 1}{x - 1}\) = \(\dfrac{(1)^2 - 1}{(1) - 1}\) = \(\dfrac{0}{0}\) (?)
Fatorando \(\dfrac{x^2 - 1}{x - 1}\), vem:
\(\dfrac{x^2 - 1}{x - 1}\) = \(\dfrac{(x + 1)(x - 1)}{x - 1}\) = x + 1
Logo, \(lim_{x \to 1} \dfrac{x^2 - 1}{x - 1}\) = \(lim_{x \to 1} (x + 1)\) = (1) + 1 = 2
Determine \(lim_{x \to 1} \dfrac{x^3 - 1}{x^2 - 1}\)
Solução
\(lim_{x \to 1} \dfrac{x^3 - 1}{x^2 - 1}\) = \(\dfrac{(1)^3 - 1}{(1)^2 - 1}\) = \(\dfrac{0}{0}\) (?)
\(\dfrac{x^3 - 1}{x^2 - 1}\) = \(\dfrac{x^3 - 1^3}{x^2 - 1}\) = \(\dfrac{(x - 1)(x^2 + x + 1)}{(x + 1)(x - 1)}\) = \(\dfrac{x^2 + x + 1}{x + 1}\)
\(lim_{x \to 1} \dfrac{x^3 - 1}{x^2 - 1}\) = \(lim_{x \to 1} \dfrac{x^2 + x + 1}{x + 1}\) = \(\dfrac{(1)^2 + (1) + 1}{(1) + 1}\) = 3/2
Determine \(lim_{x \to -2} \dfrac{8 + x^3}{4 - x^2}\)
Solução
\(lim_{x \to -2} \dfrac{8 + x^3}{4 - x^2}\) = \(\dfrac{8 + (-2)^3}{4 - (-2)^2}\) = \(\dfrac{0}{0}\) (?)
\(\dfrac{8 + x^3}{4 - x^2}\) = \(\dfrac{2^3 + x^3}{2^2 - x^2}\) = \(\dfrac{(2 + x)(2^2 - 2x + x^2)}{(2 + x)(2 - x)}\) = \(\dfrac{4 - 2x + x^2}{2 - x}\)
\(lim_{x \to -2} \dfrac{8 + x^3}{4 - x^2}\) = \(lim_{x \to -2} \dfrac{4 - 2x + x^2}{2 - x}\) = \(\dfrac{4 - 2(-2) + (-2)^2}{2 - (-2)}\) = \(\dfrac{4 + 4 + 4}{2 + 2}\) = \(\dfrac{12}{4}\) = 3/2
Considere f(x) e g(x) funções reais e a um número real.
Limite da soma é igual à soma dos limites:
\(lim_{x \to a}\) [f(x) + g(x)] = \(lim_{x \to a}\) f(x) + \(lim_{x \to a}\) g(x)
Limite da diferença é igual à diferença dos limites:
\(lim_{x \to a}\) [f(x) - g(x)] = \(lim_{x \to a}\) f(x) - \(lim_{x \to a}\) g(x)
Limite do produto é igual ao produto dos limites:
\(lim_{x \to a}\) [f(x) ∙ g(x)] = \(lim_{x \to a}\) f(x) ∙ \(lim_{x \to a}\) g(x)
Limite da divisão é igual ao quociente dos limites:
\(lim_{x \to a} \dfrac{f(x)}{g(x)}\) = \( \dfrac{lim_{x \to a} f(x)}{lim_{x \to a} g(x)}\), com \(lim_{x \to a}\) g(x) ≠ 0
Limite de potência é igual à potência do limite:
\(lim_{x \to a} [f(x)]^n\) = \(\left[lim_{x \to a} f(x)\right]^n\)
Limite de radical é igual ao radical do limite:
\(lim_{x \to a} \sqrt{f(x)}\) = \(\sqrt{lim_{x \to a} f(x)}\)
Limite de logarítmo é igual ao logarítmo do limite:
\(lim_{x \to a} ln [f(x)]\) = ln \(\left[lim_{x \to a} f(x)\right]\)
Limite de seno é igual ao seno do limite:
\(lim_{x \to a} sen [f(x)]\) = sen \(\left[lim_{x \to a} f(x)\right]\)
Limite de cosseno é igual ao cosseno do limite:
\(lim_{x \to a} cos [f(x)]\) = cos \(\left[lim_{x \to a} f(x)\right]\)
Limite de exponencial é igual à exponencial do limite:
\(lim_{x \to a} e^{f(x)}\) = \(e^{lim_{x \to a} f(x)}\)
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.