

Sistemas de inequações são compostos de duas ou mais inequações que devem ser satisfeitas ao mesmo tempo.
O conjunto solução de um sistema de inequações é determinado pela intersecção dos conjuntos soluções de cada inequação do sistema.
Determine a solução de \(\left\{\begin{array}{l} 2x - 1 \geq 5 \\ - x - 3 < 0 \end{array}\right.\)
Solução
Inequação 1: 2x - 1 ≥ 5 ⇔ 2x ≥ 6 ⇔ x ≥ 3
Inequação 2: - x - 3 < 0 ⇔ x > -3
Esquematizando as soluções e fazendo a intersecção:
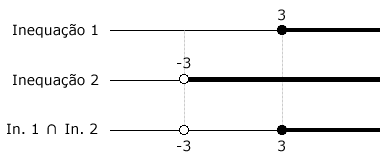
Os valores de x são comuns às duas inequações quando x ≥ 3
S = [3, ∞[ ou S = {x ∈ R | x ≥ 3}
Determine a solução de \(\left\{\begin{array}{l} 2x - 3 \leq x + 1 \\ 3x + 2 > x - 4 \end{array}\right.\)
Solução
(1): 2x - 3 ≤ x + 1 ⇔ 2x - x ≤ 1 + 3 ⇔ x ≤ 4
(2): 3x + 2 > x - 4 ⇔ 3x - x > - 4 - 2 ⇔ 2x > -6 ⇔ x > -3
Esquematizando as soluções e fazendo a intersecção:
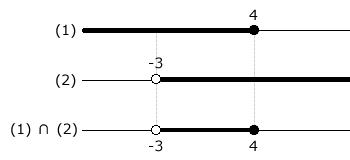
Os valores de x são comuns às duas inequações quando -3 < x ≤ 4
S = ]-3, 4] ou S = {x ∈ R | -3 < x ≤ 4}
Determine a solução de \(\left\{\begin{array}{l} x^2 - 1 < 0 \\ x^2 - 2x > 0 \end{array}\right.\)
Solução
(1): x² - 1 < 0
Fazendo x² - 1 = 0
x² = 1
x' = -1 e x" = 1
Concavidade voltada para cima.
(2): x² - 2x > 0
Fazendo x² - 2x = 0
x(x - 2) = 0
x' = 0 e x" = 2
Concavidade voltada para cima.
Esquematizando as soluções e fazendo a intersecção:
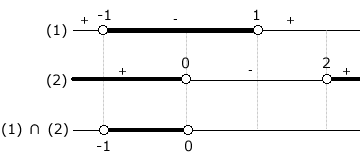
Os valores de x são comuns às duas inequações quando -1 < x < 0
S = ]-1, 0[ ou S = {x ∈ R | -1 < x < 0}
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.