

Inequação produto: são as inequações redutíveis à forma f(x) ∙ g(x) > 0 (ou <, ≥, ≤, ≠), onde f(x) e g(x) são funções na variável x.
Inequação quociente: são as inequações redutíveis à forma \( \dfrac{f(x)}{g(x)} \) > 0 (ou <, ≥, ≤, ≠), onde f(x) e g(x) são funções na variável x.
Há uma técnica especial para a resolução desses tipos de inequações: analisar os sinais das funções que compõem a inequação.
Acompanhe...
Determine os valores de x em (x - 2)(x - 3) > 0
Solução
Note que duas funções compõem o produto (x - 2)(x - 3).
Fazendo y\(_1\) = x - 2 e y\(_2\) = x - 3.
A raiz de y\(_1\) é x = 2.
Esquematicamente, tem-se:
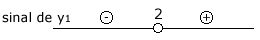
A raiz de y\(_2\) é x = 3.
Esquematicamente, tem-se:
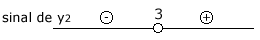
Elabora-se um quadro de sinais, como o seguinte, realizando as regras de sinais:
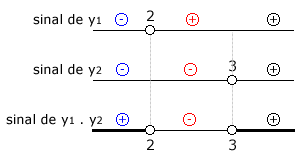
Repare nas regras de sinais em azul, vermelho e preto. O produto (x - 2)(x - 3) será positivo para x < 2 ou x > 3.
S = {x ∈ R | x < 2 ou x > 3}
Determine os valores de x em \(\dfrac{x - 2}{x - 3}\) ≤ 0
Solução
Note que duas funções compõem a razão \(\dfrac{x - 2}{x - 3}\).
Fazendo y\(_1\) = x - 2 e y\(_2\) = x - 3.
A raiz de y\(_1\) é x = 2.
Esquematicamente, tem-se:
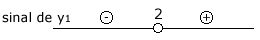
A raiz de y\(_2\) é x = 3.
Esquematicamente, tem-se:
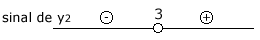
Como y\(_2\) é denominador, x ≠ 3 ("bolinha aberta").
Elabora-se um quadro de sinais, como o seguinte, realizando as regras de sinais:
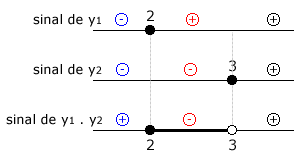
Repare nas regras de sinais em azul, vermelho e preto. O produto (x - 2)(x - 3) será positivo para x < 2 ou x > 3.
Lembrando que x = 3 ficou com a "bolinha aberta", pois x - 3 é denominador e não pode ser nulo.
S = {x ∈ R | 2 ≤ x < 3} ou S = [2, 3[
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.