Função modular é toda função do tipo

f(x) = | x |

Pela definição de módulo temos:

\( f(x) = \left\{\begin{array}{rll} x, & \hbox{se} & x \geq 0 \\ -x, & \hbox{se} & x < 0 \end{array}\right. \)

Observe que:

• o valor de x será o mesmo quando ele for positivo Ex: |3| = 3
• o valor de x será o oposto dele quando ele for negativo Ex: |-3| = -(-3) = 3

Entendi

Vamos associar alguns valores para f(x) = | x |.

Lembrando que f(x) = | x | pode ser representado como y = | x |, podemos montar a seguinte tabela:

Marcando as coordenadas (pares ordenados) no plano cartesiano teremos o seguinte gráfico:

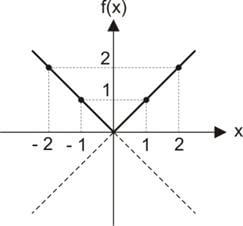
Observações:

• O domínio é real D = \( \mathbb{R} \)
• A imagem é real não negativo Im = \( \mathbb{R}_+ \)

Voltar Entendi

Determine o domínio e a imagem de f(x) = 1 + |x|

Solução

Pela definição de módulo, tem-se:

• Se x ≥ 0, a função de reduz a f(x) = 1 + x
• Se x < 0, a função de reduz a f(x) = 1 - x

Como ambas são do 1º grau, tem-se que seus gráficos são retas. Então, vamos atribuir três valores para x para obter y.

• Um valor maior do que 0 (x = 2, por exemplo):
  f(2) = 1 + (2) = 3 (foi utilizado f(x) = 1 + x pois x ≥ 0)
• x = 0
  f(0) = 1 + (0) = 1 (foi utilizado f(x) = 1 + x pois x = 0)
• Um valor menor do que 0 (x = -2, por exemplo)
  f(-2) = 1 - (-2) = 3 (foi utilizado f(x) = 1 - x pois x < 0)

Colocando esses valores numa tabela, vem:

Graficamente, tem-se:

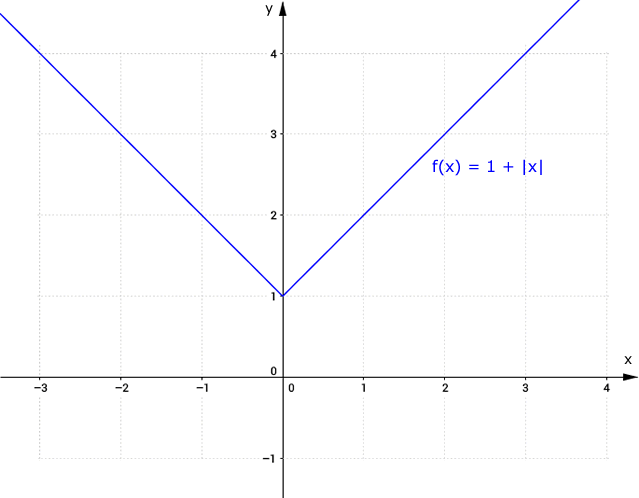
O domínio é D(f) = IR

A imagem é Im(f) = [1, ∞[

Voltar Entendi