

Sendo a um número real positivo e diferente de 1 (a > 0 e a ≠ 1), chama-se função exponencial de base a a função
f: \( \mathbb{R} \rightarrow \mathbb{R} \)
que associa a cada número real x o número \(a^x\).
f(x) = a\(^x\)
com a > 0 e a ≠ 1
Por exemplo: Na função
f(x) = 2\(^x\)
Cada valor de x (elemento do domínio) será associado a um valor 2\(^x\) (imagem).
Se x = 3, teremos
f(3) = 2\(^3\) = 8
Neste caso encontramos o par ordenado (3, 8). Lembre-se que f(x) pode ser representado por y.
E assim por diante:
| x | 2\(^x\) | Par ordenado |
|---|---|---|
| 1 | 2\(^1\) = 2 | (1, 2) |
| 2 | 2\(^2\) = 4 | (2, 4) |
| 5 | 2\(^5\) = 32 | (5, 32) |
| 8 | 2\(^8\) = 256 | (8, 256) |
Graficamente temos:

Relacione com os nomes de acordo com
f(x) = a\(^x\)
Vamos voltar ao exemplo anterior.
f(x) = 2\(^x\)
Substituindo os valores de x para encontrar 2\(^x\), podemos montar a seguinte tabela.
| x | 2\(^x\) | Par ordenado |
|---|---|---|
| -2 | 2\(^{-2}\) = 1/4 | (-2, 1/4) |
| -1 | 2\(^{-1}\) = 1/2 | (-1, 1/2) |
| 0 | 2\(^0\) = 1 | (0, 1) |
| 1 | 2\(^1\) = 2 | (1, 2) |
| 2 | 2\(^2\) = 4 | (2, 4) |
| 3 | 2\(^3\) = 8 | (3, 8) |
| 4 | 2\(^4\) = 16 | (4, 16) |
| 5 | 2\(^5\) = 32 | (5, 32) |
| 6 | 2\(^6\) = 64 | (6, 64) |
Colocando os pares ordenados no plano cartesiano teremos um gráfico do tipo:
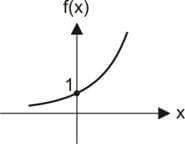
Note que ele é crescente. Isso ocorreu porque a base é maior do que 1 (2). Guarde isso:
Sempre que a base for maior do que 1, o gráfico será crescente.
a > 1 ⇔ função crescente
Observações:
E o que acontece se a base for maior do que 0 e menor do que 1?
Considere a função exponencial de base \(\left(\dfrac{1}{3}\right)^x\):
f(x) = \(\left(\dfrac{1}{3}\right)^x\)
Calculando os valores associados a cada elemento do domínio, temos:
| x | \(\left(\dfrac{1}{3}\right)^x\) | Par ordenado |
|---|---|---|
| -3 | \(\left(\dfrac{1}{3}\right)^{-3}\) = 27 | (-3, 27) |
| -2 | \(\left(\dfrac{1}{3}\right)^{-2}\) = 9 | (-2, 9) |
| -1 | \(\left(\dfrac{1}{3}\right)^{-1}\) = 3 | (-1, 3) |
| 0 | \(\left(\dfrac{1}{3}\right)^0\) = 1 | (0, 1) |
| 1 | \(\left(\dfrac{1}{3}\right)^1\) = \(\dfrac{1}{3}\) | (1, 1/3) |
| 2 | \(\left(\dfrac{1}{3}\right)^2\) = \(\dfrac{1}{9}\) | (2, 1/9) |
| 3 | \(\left(\dfrac{1}{3}\right)^3\) = \(\dfrac{1}{27}\) | (3, 1/27) |
| 4 | \(\left(\dfrac{1}{3}\right)^4\) = \(\dfrac{1}{81}\) | (4, 1/81) |
| 5 | \(\left(\dfrac{1}{3}\right)^5\) = \(\dfrac{1}{243}\) | (5, 1/243) |
Colocando os pares ordenados no plano cartesiano teremos um gráfico do tipo:
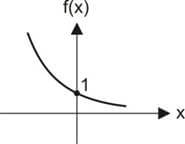
Note que ele é decrescente. Isso ocorreu porque a base é \(\dfrac{1}{3}\).
Se 0 < a < 1, o gráfico é decrescente
0 < a < 1 ⇔ função decrescente
Observe, ainda, que
O gráfico

Representa uma função exponencial:
O gráfico

Representa uma função exponencial:
A soma das corretas é
Determine o domínio e a imagem de f(x) = 2\(^x\)
Solução
Atribuindo valores para x, vem:
| x | y |
|---|---|
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
Graficamente, tem-se:
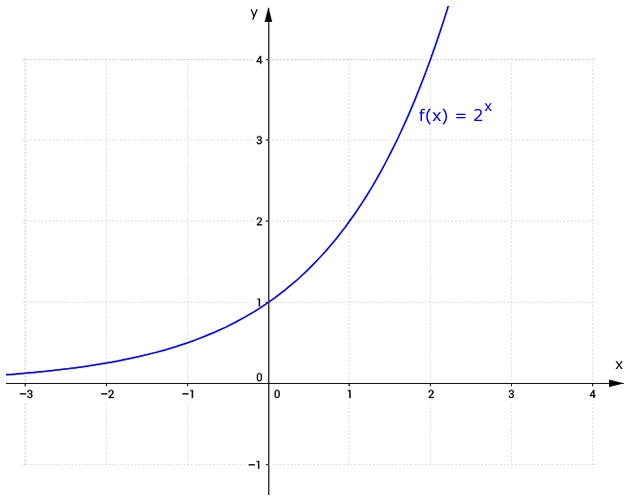
O domínio é D(f) = IR
A imagem é Im(f) = ]0, ∞[
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.