Observe o diagrama seguinte:

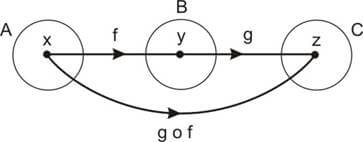
Temos uma função f que associa a cada elemento x ∈ A um único elemento y = f(x) ∈ B e uma função g que associa a cada elemento y ∈ B um único elemento z = g(y) ∈ C.

Se lembrarmos, porém, que y = f(x), veremos que o elemento z = g(y) ∈ C é, na verdade, igual a g( f(x) ). Obtemos, então, uma nova função h, de A em C, que associe o elemento x ∈ A diretamente com o elemento z = g(f(x)) ∈ C. Esta função h é chamada de função composta de g em f e é indicada por g∘f.

Então:

h(x) = g∘f (x) = g( f(x) )

Explica de outro jeito

Suponha duas funções:

• f(x) = 2x + 3
• g(x) = 5 - x

Vamos, por exemplo, determinar o valor de f(x) para x = 1. Substituindo x por 1 em f(x), temos:

f(1) = 2(1) + 3

f(1) = 2 + 3 = 5 (Só pra lembrar, 5 é a imagem de 1)

Pensando como programador, o valor de entrada foi 1 e o de saída 5.

Agora, vamos pegar esse valor que acabamos de descobrir (5) e substituir em g(x). Substituindo x por 5 em g(x), temos:

g(5) = 5 - 5

g(5) = 5 - 5 = 0 (0 é a imagem de 5)

Pensando como programador, o valor de entrada foi 5 e o de saída 0.

Repare que iniciamos com o valor 1 e chegamos no valor 0, calculando primeiramente f(x) e depois g(x).

E se quiséssemos iniciar com 2? E com 3? 4?

Daria bastante trabalho, não é mesmo?

A boa notícia é que podemos gerar uma terceira função que irá facilitar bastante o nosso trabalho. Pense:

O que acabamos de fazer foi substituir o valor de saída de f(x) em g(x). Ou seja: g( f(x) ).

Se temos que substituir o valor (primeiro valor de entrada) em f(x) para depois substituir o resultado encontrado (primeiro valor de saída que será o segundo valor de entrada) em g(x) para chegarmos no valor final (segundo valor de saída), podemos gerar uma terceira função, fazendo g( f(x) ).

g( f(x) ) = 5 - f(x)

g( 2x + 3 ) = 5 - (2x + 3)

g( 2x + 3 ) = 5 - 2x - 3

g( 2x + 3 ) = 2 - 2x

Chamando g( 2x + 3 ) de h(x), temos

h(x) = 2 - 2x (nossa terceira função)

Agora, ao invés de ter que substituir primeiro em f(x) pra depois em g(x), podemos substituir diretamente em h(x). Vamos testar com o valor do nosso exemplo?

Substituindo x = 1 em h(x) temos:

h(x) = 2 - 2x

h(1) = 2 - 2 (1)

h(1) = 2 - 2 = 0 (mesmo resultado)

Podemos determinar o valor final com outras entradas de forma bem mais rápida e fácil. Legal, não é?

A nova função h(x) foi determinada pela composição das funções f(x) e g(x). Representamos por:

h(x) = g∘f (x) = g( f(x) )

Pra praticar e ficar bem afiado, utilize outros valores. Calcule primeiramente em f(x) e depois em g(x). Compare o resultado substituindo o valor escolhido em h(x).

Voltar Muito legal

Sendo g:R → R e f:R → R definidas por g(x) = 3x - 1 e f(x) = x² + 5, determine g( f(x) ) e f( g(x) )

Solução

Substituindo x por f(x) em g(x) = 3x - 1:

g( f(x) )

3( f(x) ) - 1

3( x² + 5 ) - 1

3x² + 15 - 1

3x² + 14

Substituindo x por g(x) em f(x) = x² + 5:

f( g(x) )

( 3x - 1 )² + 5

9x² - 6x + 1 + 5

9x² - 6x + 6

Voltar Entendi