

Inequações trigonométricas são inequações que envolvem funções trigonométricas.
Exemplos:
Resolva a inequação sen x < -\(\dfrac{\sqrt{2}}{2}\)
Solução
Identificamos, no gráfico, -\(\dfrac{\sqrt{2}}{2}\) no eixo dos senos.
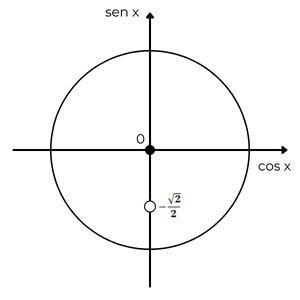
Utilizamos bolinha aberta porque -\(\dfrac{\sqrt{2}}{2}\) não pode estar incluído, já que o enunciado informou valores menores que ele.
O próximo passo é obter os valores cujo seno é menor que -\(\dfrac{\sqrt{2}}{2}\).
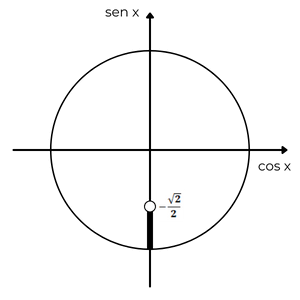
Identificamos, com o auxílio de uma linha tracejada, os ângulos compreendidos entre 0º e 360º cujos senos valem -\(\dfrac{\sqrt{2}}{2}\).
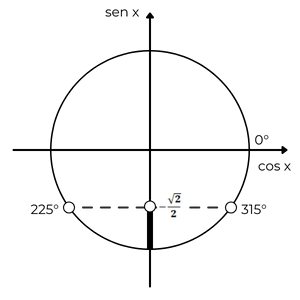
Encontramos os ângulos 225º e 315º, pois sen 225º = sen 315º = -\(\dfrac{\sqrt{2}}{2}\). Utilizamos bolinhas abertas porque eles não podem estar inclusos na solução.
O gráfico abaixo apresenta os valores cujo seno é menor que -\(\dfrac{\sqrt{2}}{2}\).
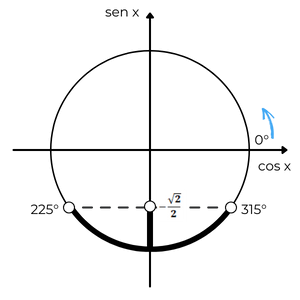
Note que as soluções são os arcos compreendidos entre 225º e 315º, considerando a primeira volta (0º a 360º).
A solução geral é dada por:
S = {x ∈ \(\mathbb{R}\) | 225º + k ∙ 360º < x < 315º + k ∙ 360º, k ∈ \(\mathbb{Z}\)}
Resolva a inequação sen x < -\(\dfrac{3}{2}\)
Solução
A circunferência trigonométrica possui raio igual a 1. Logo, tanto sen(x) como cos(x) variam entre -1 e 1.

Como -\(\dfrac{3}{2}\) < -1 e -1 < sen(x) < 1, a inequação não admite solução.
Portanto, S = { }
Resolva a inequação cos x ≥ \(\dfrac{1}{2}\), sabendo que x ∈ [0º, 360º]
Solução
Primeiramente, identificamos no gráfico o valor \(\dfrac{1}{2}\) no eixo dos cossenos.
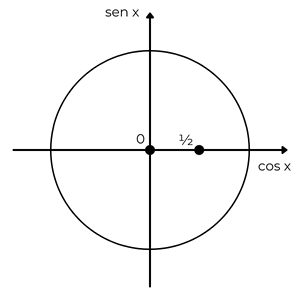
Note que representamos \(\dfrac{1}{2}\) com bolinha fechada pois queremos valor maior ou igual a \(\dfrac{1}{2}\).
Agora, obtemos os valores cujo cosseno é maior ou igual a \(\dfrac{1}{2}\).
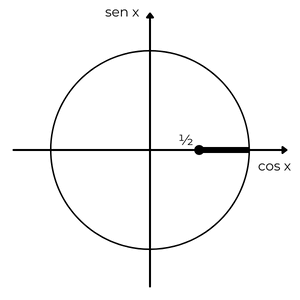
Identificamos, com o auxílio de uma linha tracejada, os ângulos compreendidos entre 0º e 360º cujos cossenos valem \(\dfrac{1}{2}\).

Encontramos os ângulos 60º e 300º, pois cos 60º = cos 300º = \(\dfrac{1}{2}\).
Por fim, identificamos o intervalo dos ângulos cujos cossenos são maiores ou iguais a \(\dfrac{1}{2}\).

As soluções são os arcos compreendidos entre 0º e 60º e entre 300º e 360º. Note que 0º, 60º, 300º e 360º estão incluídos na solução (por isso estão representados com bolinhas fechadas).
Como o domínio é [0º, 360º], temos a solução:
S = [0º, 60º] ∪ [300º, 360º]
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.