

Esfera é um sólido gerado pela rotação de um semicírculo em torno de um eixo que contém seu diâmetro.
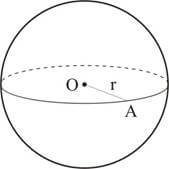
Elementos:
Superfície esférica é a superfície gerada pela rotação completa de uma semicircunferência em torno de um eixo que contém as extremidades de seu diâmetro.
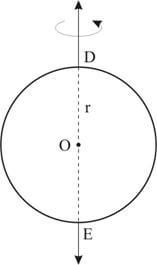
Secção plana é a intersecção de uma esfera com um plano que passa por um ponto interno dessa esfera.
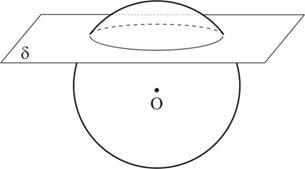
O plano que determina uma secção numa esfera é chamado de plano secante.
Toda secção plana de uma esfera é um círculo.
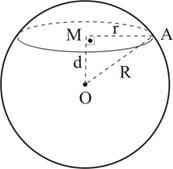
Se o plano secante não passa pelo centro da esfera, a secção é chamada de círculo menor da esfera.
Se o plano secante passa pelo centro da esfera, a secção é chamada de círculo maior ou secção meridiana da esfera.
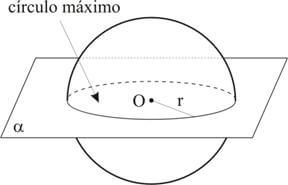
A área da superfície esférica é igual a quatro vezes a área de um círculo máximo dessa esfera.
S = 4 ∙ π ∙ r²
Uma esfera tem raio medindo 6 cm. Determine a área de sua superfície.
Solução
S = 4 ∙ π ∙ r²
S = 4 ∙ π ∙ 6²
S = 4 ∙ π ∙ 36
S = 144π cm²
O volume de uma esfera é dado por
V = \( \dfrac{4}{3} \) ∙ π ∙ r³
Uma esfera tem raio medindo 3 m. Determine seu volume.
Solução
V = \( \dfrac{4}{3} \cdot \pi \cdot r^3 \)
V = \( \dfrac{4}{3} \cdot \pi \cdot 3^3 \)
V = \( \dfrac{4}{3} \cdot \pi \cdot 27 \)
V = 36π m³
A área da superfície de uma esfera é 16π cm². Determine o raio e o volume da esfera.
Solução
Sabe-se que S = 4πr²
Segundo o enunciado, S = 16π cm²
Então:
4πr² = 16π
r² = 4
r = 2 cm
O volume da esfera é determinado por:
V = \( \dfrac{4}{3} \cdot \pi \cdot r^3 \)
\( \dfrac{4}{3} \cdot \pi \cdot 2^3 \)
\( \dfrac{4}{3} \cdot \pi \cdot 8 \)
\(\dfrac{32\pi}{3}\) cm³
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.