

Dados dois pontos A(\(x_A\); \(y_A\)) e B(\(x_B\); \(y_B\)), é possível calcular a equação da reta que passa por esses dois pontos através do determinante construído com suas coordenadas (dos pontos), igualando-o a zero.
\( \left| \begin{array}{ccc} x_A & y_A & 1 \\ x_B & y_B & 1 \\ x & y & 1 \end{array} \right| = 0 \)
Determine a equação da reta determinada pelos pontos A(2, 4) e B(5, 2).
Solução
Para determinar a equação formada pelos ponto A e B, tem-se que:
\( \left| \begin{array}{ccc} x_A & y_A & 1 \\ x_B & y_B & 1 \\ x & y & 1 \end{array} \right| = 0 \)
\( \left| \begin{array}{ccc} 2 & 4 & 1 \\ 5 & 2 & 1 \\ x & y & 1 \end{array} \right| = 0 \)
4 + 4x + 5y - 2x - 2y - 20 = 0
2x + 3y - 16 = 0
Determine a equação da reta que corta o eixo das abscissas em x = 3 e das ordenadas em y = -2.
Solução
Como a reta corta o eixo x em x = 3, tem-se que o ponto de intersecção é (3, 0), pois y = 0 (corta o eixo x quando y = 0).
Como a reta corta o eixo y em y = -2, tem-se que o ponto de intersecção é (0, -2), pois x = 0 (corta o eixo y quando x = 0).
Então:
\( \left| \begin{array}{ccc} 3 & 0 & 1 \\ 0 & -2 & 1 \\ x & y & 1 \end{array} \right| = 0 \)
-6 + 0 + 0 - (-2x) - 3y - 0 = 0
2x - 3y - 6 = 0
Observação: Toda reta do plano cartesiano pode ser representada por uma equação do tipo
a ∙ x + b ∙ y + c = 0
onde a, b e c são números reais, desde que a e b não sejam simultaneamente nulos.
Reciprocamente, toda equação do tipo a ∙ x + b ∙ y + c = 0, com a e b não simultaneamente nulos, representa uma reta do plano cartesiano.
Dada a reta de equação r: 3x - 2y + 12 = 0, determine os pontos em que r intercepta os eixos cartesianos.
Solução
A reta r intercepta o eixo das abscissas quando y = 0:
3x - 2(0) + 12 = 0
3x = -12
x = -4
(-4, 0)
A reta r intercepta o eixo das ordenadas quando x = 0:
3(0) - 2y + 12 = 0
-2y = -12
y = 6
(0, 6)
Os pontos de intersecção são (-4, 0) e (0, 6)
Em geometria plana, duas retas que não são paralelas são concorrentes e tem um único ponto comum. Vejamos como, em geometria analítica, determinamos as coordenadas desse ponto a partir das equações das duas retas.
Sejam as retas r: ax + by + c = 0 e s: dx + ey + f = 0 e r × s (concorrentes) no ponto P.
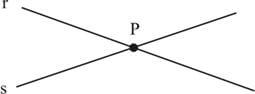
Para determinar as coordenadas de P, resolve-se o sistema
\( \left\{ \begin{array}{l} ax + by + c = 0 \\ dx + ey + f = 0 \end{array}\right. \)
onde a solução (x, y) é a coordenada de P.
Obter o ponto de intersecção das retas de equações 3x + y - 1 = 0 e x - y + 3 = 0.
Solução
O ponto de intersecção é comum as duas retas. Logo, basta resolver o sistema formado por suas equações:
\( \left\{ \begin{array}{l} 3x + y - 1 = 0 \\ x - y + 3 = 0 \end{array}\right. \)
Repare que na primeira equação tem y e na segunda -y. Assim, pode-se eliminar y somando a primeira equação com a segunda:
3x + x + y - y - 1 + 3 = 0
4x = -2
x = -1/2
Substituindo x = -1/2 na segunda equação, vem:
(-1/2) - y + 3 = 0
y = 5/2
O ponto de intersecção é P(-1/2, 5/2)
O ângulo θ determinado pelo semi-eixo positivo das abscissas e a reta r, medido no sentido anti-horário, é a inclinação dessa reta.
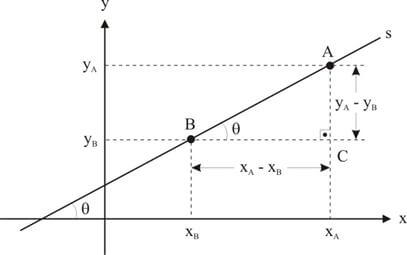
Coeficiente angular ou declividade de uma reta r não vertical é, por definição, a tangente do seu ângulo de inclinação θ.
Costuma-se indicar o coeficiente angular pela letra m. Então:
m = tg θ
Determine o coeficiente angular e a inclinação de uma reta que passa pelos A(1, 3) e B(5, 7).
Solução
Coeficiente angular:
m = \(\dfrac{y_A - y_B}{x_A - x_B}\) = \(\dfrac{3 - 7}{1 - 5}\) = 1
Inclinação (ângulo cuja tangente é igual ao coeficiente angular):
tg θ = 1
θ = arctg 1 = 45º
Seja a reta r: a ∙ x + b ∙ y + c = 0. Isolando y, vem:
y = -\(\dfrac{a}{b}\)x - \(\dfrac{c}{b}\)
Chamando de -\(\dfrac{a}{b}\) de m e -\(\dfrac{c}{b}\) de n, tem-se a forma reduzida da reta r:
y = m ∙ x + n
Determine a equação reduzida da reta 3x + y - 4 = 0.
Solução
3x + y - 4 = 0
y = -3x + 4
Determine a equação reduzida da reta paralela ao eixo das abscissas e que passa pelo ponto (3, 2).
Solução
Como a reta é paralela ao eixo x e passa pelo ponto (3, 2), tem-se que sua equação reduzida é y = 2
Considere-se uma reta r que intercepta o eixo x no ponto P(p, 0) e o eixo y no ponto Q(0, q), com p ≠ 0 e q ≠ 0.
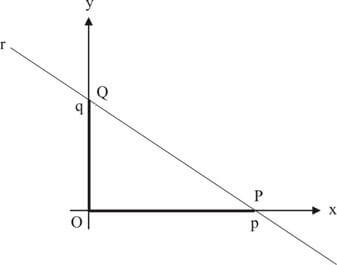
A equação da reta r pode ser escrita na forma:
\( \dfrac{x}{p} + \dfrac{y}{q} = 1 \)
Determine a equação segmentária da reta formada pelos os pontos A(0, 2) e B(3, 0).
Solução
\( \dfrac{x}{p} + \dfrac{y}{q} \) = 1
\( \dfrac{x}{3} + \dfrac{y}{2} \) = 1
O ponto A intercepta o eixo das abscissas em 5 e o ponto B intercepta o eixo das ordenadas em y = 2. Determine a equação segmentária da reta formada pelos os pontos A e B.
Solução
\( \dfrac{x}{p} + \dfrac{y}{q} \) = 1
\( \dfrac{x}{5} + \dfrac{y}{2} \) = 1
Enquanto as equações geral, reduzida e segmentária de uma reta relacionam numa única equação as coordenadas x e y de um ponto da reta, as equações paramétricas dão as coordenadas x e y em função de uma outra variável real t que é chamado parâmetro.
Determine a equação geral da reta r, cujas equações paramétricas são x = t/2 e y = t + 1.
Solução
Tem-se um sistema onde a primeira equação pode ser escrita como:
x = t/2
t = 2x
Substituindo na segunda equação, vem:
y = t + 1
y = (2x) + 1
y - 2x - 1 = 0
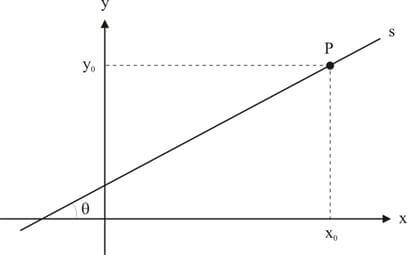
Sejam (x; y) as coordenadas de um ponto qualquer pertencente à reta. Pela definição de coeficiente angular, temos:
\( (y – y_0) = m \cdot (x – x_0) \)
Determine a equação da reta cuja inclinação é 135º e passa pelo ponto P(2, 1).
Solução
m = tg 135º = -1
\( (y – y_0) = m \cdot (x – x_0) \)
(y – 1) = (-1) ∙ (x – 2)
y – 1 = -x + 2
x + y - 3 = 0
Duas retas distintas de um plano podem ser:
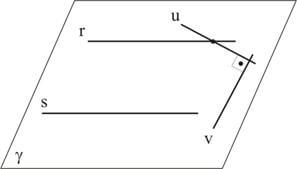
Para reconhecermos as posições de duas (ou mais) retas, basta compararmos os coeficientes angulares das mesmas:
Determine o valor de k para que as retas 3x + 2y - 1 = 0 e kx - 4y + 5 = 0 sejam
Solução
a) Para serem paralelas, os coeficientes angulares devem ser iguais.
Igualando os coeficientes angulares, vem:
k/4 = -3/2
k = -12/2 = -6
b) Para serem concorrentes, os coeficientes angulares devem ser diferentes.
Logo, k ≠ -6
c) Para serem perpendiculares, o coeficiente angular de uma reta deve ser igual ao oposto do inverso do coeficiente angular da outra:
\(m_r = -\dfrac{1}{m_s}\)
\(\dfrac{k}{4} = -\dfrac{1}{-3/2}\)
\(\dfrac{k}{4} = \dfrac{2}{3}\)
k = 8/3

\( tg \alpha = \left| \dfrac{m_r – m_s}{1 + m_r \cdot m_s} \right| \)
\( d_{P, r} = \dfrac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} \)
Determine a distância entre o ponto P(0, 0) e a reta 3x + 2y - 1 = 0.
Solução
\( d_{P, r} = \dfrac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} = \dfrac{|3 \cdot 0 + 2 \cdot 0 - 1|}{\sqrt{3^2 + 2^2}} = \dfrac{1}{\sqrt{13}} \) = \( \dfrac{\sqrt{13}}{13} \)
Determine a distância entre o ponto P(1, 3) e a reta x + y = 4.
Solução
A equação geral da reta x + y = 4 é x + y - 4 = 0
\( d_{P, r} = \dfrac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} = \dfrac{|1 \cdot 1 + 1 \cdot 3 - 4|}{\sqrt{1^2 + 1^2}} = \dfrac{0}{\sqrt{2}} \) = 0
Como a distância é zero, significa que o ponto P(1, 3) pertence à reta x + y = 4.
Determine a distância entre as retas r: 4x + 3y + 17 = 0 e s: 4x + 3y + 2 = 0.
Solução
Para determinar a distância entre as duas retas, basta obter um ponto pertencente à uma delas e calcular a distância desse ponto à outra reta.
Um ponto de r:
Para y = 1
4x + 3(1) + 17 = 0
4x = -20
x = -5
Tem-se que o ponto (-5, 1) pertence à reta r.
Calculando a distância entre (-5, 1) e a reta s: 4x + 3y + 2 = 0, vem:
\( d_{P, r} = \dfrac{|4 \cdot (-5) + 3 \cdot 1 + 2|}{\sqrt{4^2 + 3^2}} = \dfrac{|-20 + 3 + 2|}{\sqrt{25}} = \dfrac{15}{5} \) = 3
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.