

Consideremos uma circunferência de centro C(a, b) e raio R.
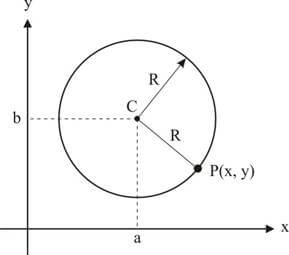
Utilizando a fórmula da distância entre dois pontos, obtemos a equação reduzida da circunferência:
(x - a)² + (y - b)² = R²
Determine a equação reduzida da circunferência de centro (1, 2) e que passa pelo ponto (4, 6).
Solução
Para obter o raio, basta calcular a distância entre os dois pontos:
r² = (4 - 1)² + (6 - 2)²
r = \(\sqrt{9 + 16}\) = 5
Como (x - a)² + (y - b)² = R², tem-se:
(x - 1)² + (y - 2)² = 5²
(x - 1)² + (y - 2)² = 25
Desenvolvendo a equação reduzida da circunferência obtemos a equação normal da circunferência. Acompanhe:
(x - a)² + (y - b)² = R²
x² + y² - 2ax - 2by + a² + b² – R² = 0
Determine o valor de k, sabendo que o ponto A(k, 1) percente à circunferência (λ) (x - 3)² + (y + 2)² = 25.
Solução
Como A pertence a circunferência λ, suas coordenadas a equação de λ:
(x - 3)² + (y + 2)² = 25
(k - 3)² + (1 + 2)² = 25
Desenvolvendo vem:
k² - 6k + 9 + 9 = 25
k² - 6k - 7 = 0
Dois números cuja soma é 6 e o produto -7:
k' = -1 e k" = 7
Determine o raio e o centro da circunferência x² + y² - 2x + 4y - 11 = 0.
Solução
A equação normal da circunferência de centro C(a, b) e raio R é:
x² + y² - 2ax - 2by + a² + b² – R² = 0
Comparando com a equação dada no enunciado, vem:
Calculando a e b, vem:
Logo, o centro é (1, -2)
Substituindo a = 1 e b = -2 em a² + b² - R² = -11, vem:
a² + b² - R² = -11
1² + (-2)² - R² = -11
1 + 4 - R² = -11
R² = 16 ⇔ R = 4
Uma equação do 2º grau em x e em y representa uma circunferência quando:
Consideremos uma circunferência β cuja equação é dada por (x - a)² + (y - b)² = r². Em relação a β, um ponto P(\(x_0\), \(y_0\)) do plano irá:
pertencer a β se e só se PC = r.
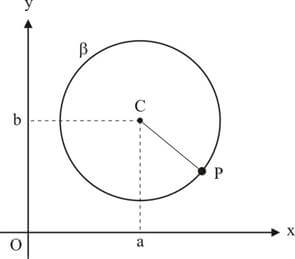
ser interior a β se e só se PC < r.
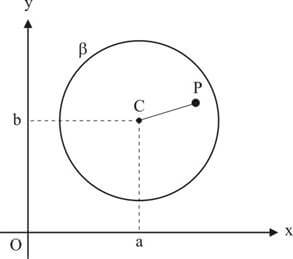
ser exterior a β se e só se PC > r.
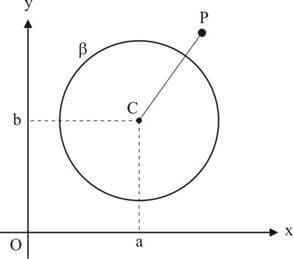
Para determinar a posição de um ponto P à uma circunferência β, basta determinar a distância entre o ponto P e o centro de β e comparar com o raio de β.
Dada a circunferência x² + y² + 2x - 2y - 7 = 0, determine a posição do ponto (2, 1) em relação à circunferência.
Solução
Basta substituir as coordenadas do ponto na equação da circunferência:
(2)² + (1)² + 2(2) - 2(1) - 7 = 4 + 1 + 4 - 2 - 7 = 0
Como deu zero, o ponto pertence à circunferência
Dada a circunferência (β) x² + y² + 2x - 2y - 7 = 0, determine a posição dos pontos A(0, 1) e B(3, 1) em relação à β.
Solução
Para A(0, 1):
(0)² + (1)² + 2(0) - 2(1) - 7 = 1 - 2 - 7 = -8 < 0
Como -8 é menor do que 0, o ponto A é interior à β
Para B(3, 1):
(3)² + (1)² + 2(3) - 2(1) - 7 = 9 + 1 + 6 - 2 - 7 = 7 > 0
Como 7 é maior do que 0, o ponto B é exterior à β
Se α é uma circunferência e r uma reta, podem ocorrer três situações:
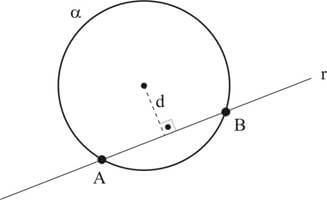
r secante a α: a reta e a circunferência tem dois pontos comuns e a distância do centro C da circunferência à reta r é menor que o raio R;
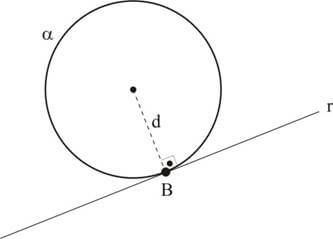
r tangente a α: a reta e a circunferência têm um único ponto comum, chamado de ponto de tangência e a distância do centro C da circunferência à reta r é igual ao raio R;
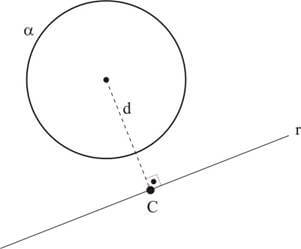
r externo a α: neste caso, não existe ponto comum entre a reta r e a circunferência α e a distância do centro C da circunferência à reta r é maior do que o raio R.
Para verificar a posição de uma reta r à uma circunferência α, há duas maneiras:
Para determinar as coordenadas dos pontos de intersecção de uma circunferência com uma reta, basta resolver o sistema formado pelas equações da reta e da circunferência.
Determine a posição relativa entre a circunferência x² + y² = 2 e a reta y = -x + 1.
Solução
Modo utilizado: comparação entre o raio da circunferência e a distância do centro da mesma com a reta
Da equação da circunferência x² + y² = 2, obtém-se:
A equação da reta pode ser escrita como x + y - 1 = 0.
d = \(\dfrac{|0 + 0 + 1|}{\sqrt{1^2 + 1^2}} = \dfrac{1}{\sqrt{2}} = \dfrac{\sqrt{2}}{2}\)
Como d < r, a reta é secante à circunferência
Determine a equação da circunferência de centro C(1, 2) e tangente à reta (r) 3x + 4y + 4 = 0.
Solução
Como r é tangente à circunferência, o raio da circunferência é igual a distância do centro da mesma até r.
d = r = \(\dfrac{|3 \cdot 1 + 4 \cdot 2 + 4|}{\sqrt{3^2 + 4^2}} = \dfrac{15}{5} \) = 3
Portanto, a equação da circunferência é (x - 1)² + (y - 2)² = 9
Dadas duas circunferências, uma de centro \( C_1 \) e raio \(R_1\) e a outra de centro \(C_2\) e raio \(R_2\), compararemos o seguimento de reta \( C_1 C_2 \) e \( R_1 + R_2 \).
Há três possibilidades:
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.