

Já ouviu falar em cônicas?
Se não, você vai ver que elas são bem familiares...
Sejam:
Uma elipse (ε) é o conjunto dos pontos de α cuja soma das distâncias a F\(_1\) e F\(_2\) é uma constante 2a maior que 2c.
P ∈ ε ⇔ PF\(_1\) + PF\(_2\) = 2a
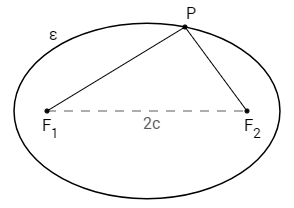
onde:
a) A elipse tem dois eixos de simetria \(A_1A_2\) e \(B_1B_2\), perpendiculares em C. C é o ponto médio de ambos os eixos. \(A_1A_2\) é chamado eixo maior, \(B_1B_2\) é chamado eixo menor e C é chamado centro da elipse.
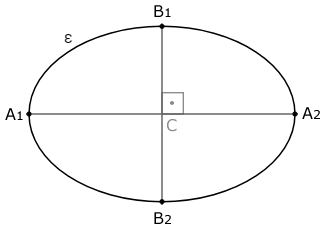
b) O eixo maior \(A_1A_2\) tem medida 2a
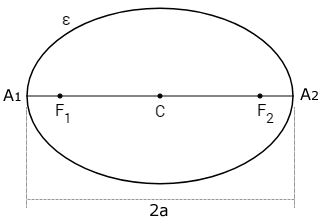
c) Os segmentos \(B_1F_1\) e \(B_1F_2\) tem medida a
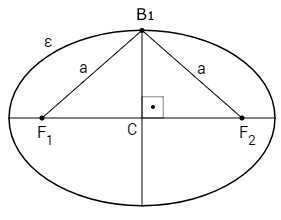
d) Relação fundamental:
Sendo \(B_1B_2\) = 2b, então \(B_1C\) = b, tem-se:
\(a^2 = b^2 + c^2\)
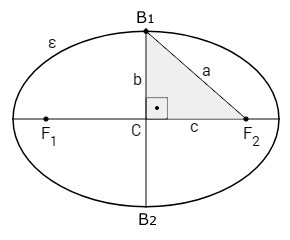
e) Excentridade da elipse: e = \(\dfrac{c}{a}\), 0 < e < 1
1º Caso: eixo maior paralelo ao eixo x
\(\dfrac{(x - x_0)^2}{a^2} + \dfrac{(y - y_0)^2}{b^2} = 1\)
2º Caso: eixo maior paralelo ao eixo y
\(\dfrac{(y - y_0)^2}{a^2} + \dfrac{(x - x_0)^2}{b^2} = 1\)
Determine a equação reduzida da elipse
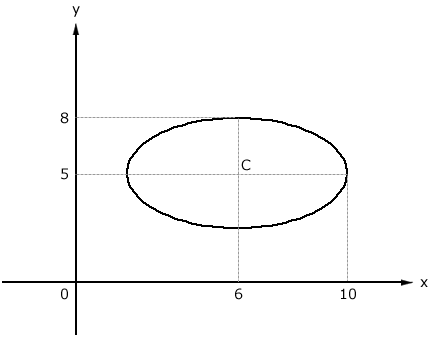
Solução
Assim:
\(\dfrac{(x - 6)^2}{4^2} + \dfrac{(y - 5)^2}{3^2} = 1\)
\(\dfrac{(x - 6)^2}{16} + \dfrac{(y - 5)^2}{9} = 1\)
Determine a equação reduzida da elipse
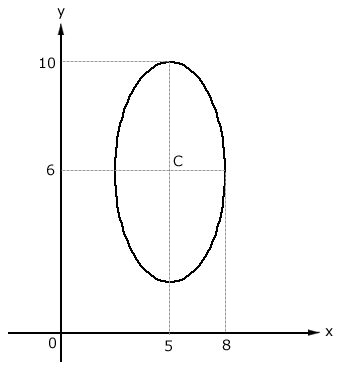
Solução
Assim:
\(\dfrac{(y - 6)^2}{4^2} + \dfrac{(x - 5)^2}{3^2} = 1\)
\(\dfrac{(y - 6)^2}{16} + \dfrac{(x - 5)^2}{9} = 1\)
Na figura abaixo, o ponto P pertence à elipse de focos F\(_1\) e F\(_2\). Determine a equação reduzida da elipse.
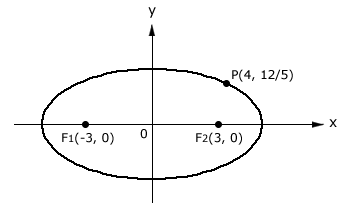
Solução
O centro C é o ponto médio de F\(_1\)F\(_2\): C(0, 0)
Sendo 2a o eixo maior, então:
2a = PF\(_1\) + PF\(_2\)
2a = \(\sqrt{(4 + 3)^2 + (12/5 - 0)^2} + \sqrt{(4 - 3)^2 + (12/5 - 0)^2}\)
2a = \(\sqrt{49 + 144/25} + \sqrt{1 + 144/25}\)
2a = \(\sqrt{1369/25} + \sqrt{169/25}\)
2a = 37/5 + 13/5
2a = 50/5
2a = 10
a = 5
Sendo b a medida do semi-eixo menor, tem-se:
a² = b² + c²
5² = b² + 3²
b² = 25 - 9 = 16
b = 4
Assim:
\(\dfrac{(x - 0)^2}{5^2} + \dfrac{(y - 0)^2}{4^2} = 1\)
\(\dfrac{x^2}{25} + \dfrac{y^2}{16} = 1\)
Sejam:
Uma hipérbole (H) é o conjunto dos pontos de α cuja diferença, em valor absoluto, das distâncias a F\(_1\) e F\(_2\) é uma constante 2a menor que 2c:
P ∈ H ⇔ |PF\(_1\) - PF\(_2\)| = 2a
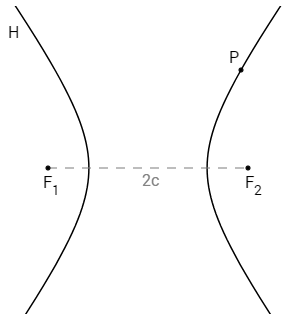
onde:
a) A hipérbole tem dois eixos de simetria \(A_1A_2\) e \(B_1B_2\), perpendiculares em C. C é o ponto médio de ambos os eixos. \(A_1A_2\) é chamado eixo real, \(B_1B_2\) é chamado eixo imaginário e C é chamado centro da hipérbole.
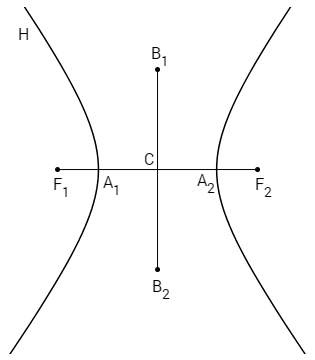
b) O eixo real \(A_1A_2\) tem medida 2a
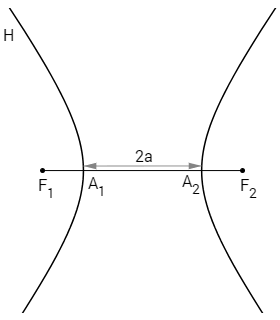
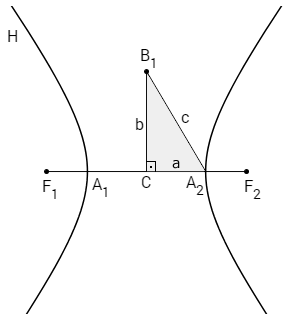
c) O ponto \(B_1\) é tal que os segmentos \(B_1A_1\) e \(B_1A_2\) tem medida c.
Sendo \(B_1B_2\) = 2b, então \(B_1C\) = b, tem-se:
\(c^2 = a^2 + b^2\)
e) Excentridade da hipérbole: e = \(\dfrac{c}{a}\), e > 1
Quando a = b, a hipérbole é chamada de hipérbole equilátera e sua excentricidade é \(\sqrt{2}\)
1º Caso: eixo real paralelo ao eixo x
\(\dfrac{(x - x_0)^2}{a^2} - \dfrac{(y - y_0)^2}{b^2} = 1\)
2º Caso: eixo real paralelo ao eixo y
\(\dfrac{(y - y_0)^2}{a^2} - \dfrac{(x - x_0)^2}{b^2} = 1\)
Na figura abaixo, o ponto P pertence à hipérbole de focos F\(_1\) e F\(_2\). Sabendoq que F\(_1\) = (-\(\sqrt{5}\), 0), F\(_2\) = (\(\sqrt{5}\), 0) e P = (\(\sqrt{5}\), 4), determine a equação reduzida da hipérbole.
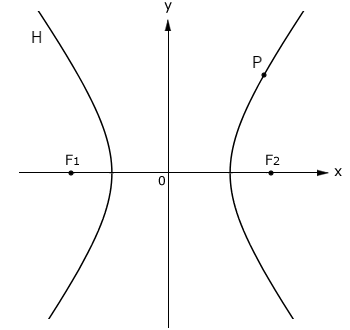
Solução
O centro C da hipérbole é o ponto médio de F\(_1\)F\(_2\). Logo C(0, 0).
Sendo 2a a medida do eixo real, tem-se:
2a = |PF\(_1\) - PF\(_2\)|
2a = |\(\sqrt{(\sqrt{5} + \sqrt{5})^2 + (4 - 0)^2} - \sqrt{(\sqrt{5} - \sqrt{5})^2 + (4 - 0)^2}\)|
2a = |\(\sqrt{(2\sqrt{5})^2 + (4)^2} - \sqrt{(0)^2 + (4)^2}\)|
2a = |\(\sqrt{36} - \sqrt{16}\)|
2a = |6 - 4| = |2| = 2
a = 1
Sendo b a medida do semi-eixo imaginário, tem-se:
c² = a² + b²
\(\sqrt{5}^2 = 1^2 + b^2\)
\(b^2 = \sqrt{5}^2 - 1^2\)
\(b^2\) = 5 - 1 = 4
b = 2
\(\dfrac{(x - 0)^2}{1^2} - \dfrac{(y - 0)^2}{2^2} = 1\)
\(\dfrac{x^2}{1} - \dfrac{y^2}{4} = 1\)
Sejam num plano α uma reta d e um ponto fixo F não pertencente a d.
Uma parábola (ρ) é o conjunto dos pontos de α que equidistam de F e d.
P ∈ y ⇔ PF = PP'
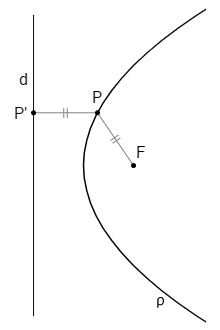
onde:
A parábola possui um eixo (e) de simetria passando por F e perpendicular à diretriz d.
V é chamado de vértice da parábola, FF' é chamado parâmetro da parábola e FV = VF' = p/2 (V equidista de F e d)
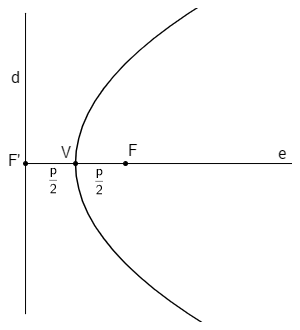
1º Caso: eixo de simetria paralelo ao eixo x
Concavidade para a direita:
\((y - y_0)^2 = 2p (x - x_0)\)
Concavidade para a esquerda:
\((y - y_0)^2 = -2p (x - x_0)\)
2º Caso: eixo de simetria paralelo ao eixo y
Concavidade para cima:
\((x - x_0)^2 = 2p (y - y_0)\)
Concavidade para baixo:
\((x - x_0)^2 = -2p (y - y_0)\)
Determine a equação reduzida da parábola abaixo sabendo que F'(1, 4) e F(5, 4).
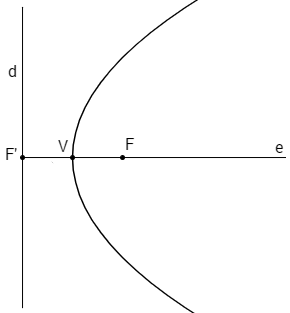
Solução
O vértice V é determinado por:
Logo, V(3, 4)
O parâmetro é dado pela distância de F a d: p = 5 - 1 = 4
Assim:
(y - 4)² = 8(x - 3)
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.