

Para a construção de números complexos, admite-se a existência de um número, representado por i e denominado unidade imaginária, onde
i² = -1
Observe as seguintes potências:
Reparou que a partir do expoente 4 os valores das potências se repetem?
Os valores das potências de i sempre se repetem. Os resultados possíveis são:
-1, 1, -i e i
Portanto, dado n ∈ \( \mathbb{N} \), a potência i\(^n\) será um destes quatro valores. Para descobrir qual desses valores ocorrerá, basta dividir o número n por 4. Tem-se, então:
i\(^n\) = i\(^r\) onde r é o resto da divisão de n por 4
Exemplo:
i\(^{26}\) = ?
Para determinar o valor de i\(^{26}\), basta obter o resto da divisão 26 por 4. O resto desta divisão é 2. Logo:
i\(^{26}\) = i² = -1
i\(^{47}\) =
Dados dois números reais a e b, chama-se número complexo o número
z = a + bi
onde i é a unidade imaginária.
Considere o número complexo z = a + bi.
Quem é a unidade imaginária do número complexo z = 2 - 5i?
Considerando o número complexo z = -3 + 7i, ligue os itens com seus significados.
Selecione um item acima e depois selecione o item correspondente abaixo.
Se z = a + bi é um número complexo qualquer, seu conjugado é
\( \bar{z} \) = a - bi
Note que inverteu o sinal da parte imaginária.
Para obter o conjugado de um nº complexo z basta inverter o sinal de
O conjugado do número complexo z = 2 - 5i é
O nº complexo de \( \bar{z} \) = - 12 + 8i é
Sejam z\(_1\) = a + bi e z\(_2\) = c + di.
Se z\(_1\) = z\(_2\), tem-se que a + bi = c + di.
Então a = c e b = d.
Sabendo que:
podemos concluir que b + c vale:
Agora iremos trabalhar um pouco com as operações de números complexos. Está pronto?
Seja z\(_1\) = a + bi e z\(_2\) = c + di.
z\(_1\) + z\(_2\) = (a + bi) + (c + di) = (a + c) + (b + d)i
Exemplo: Sejam A = 8 + 5i e B = 7 + 4i.
A + B = 8 + 5i + 7 + 4i = (8 + 7) + (5 + 4)i = 15 + 9i
Sabendo que:
Quanto vale z\(_1\) + z\(_2\)?
Sejam z\(_1\) = a + bi e z\(_2\) = c + di.
z\(_1\) - z\(_2\) = (a + bi) - (c + di) = (a - c) + (b - d)i
Exemplo: Sejam A = 8 + 5i e B = 7 + 4i.
A - B = 8 + 5i - (7 + 4i) = 8 + 5i - 7 - 4i = (8 - 7) + (5 - 4)i = 1 + i
Sabendo que:
Quanto vale z\(_1\) - z\(_2\)?
Sejam z\(_1\) = a + bi e z\(_2\) = c + di.
z\(_1\) ∙ z\(_2\) = (a + bi) ∙ (c + di) = (ac - bd) + (ad + bc)i
Vale ressaltar que o resultado foi obtido efetuando a multiplicação:
(a + bi) ∙ (c + di) = ac + adi + cbi + bdi² = ac + (ad + bc)i - bd = (ac - bd) + (ad + bc)i
Exemplo: Sejam A = 8 + 5i e B = 7 + 4i.
A ∙ B = (8 + 5i) ∙ (7 + 4i) = (8 ∙ 7 - 5 ∙ 4) + (8 ∙ 4 + 5 ∙ 7)i = (56 - 20) + (32 + 35)i = 36 + 67i
Se preferir, A ∙ B pode ser feito passo-a-passo:
A ∙ B = (8 + 5i) ∙ (7 + 4i) = 8 ∙ 7 + 8 ∙ 4i + 5i ∙ 7 + 5i ∙ 4i = 56 + 32i + 35i + 20i² = 56 + 67i - 20 = 36 + 67i
Sejam z\(_1\) = a + bi e z\(_2\) = c + di.
Para efetuar a divisão \( \dfrac{z_1}{z_2} = \dfrac{a + bi}{c + di} \) multiplica-se o numerador e o denominador pelo conjugado do denominador.
\( \dfrac{z_1}{z_2} \cdot \dfrac{\bar{z_2}}{\bar{z_2}} = \dfrac{a + bi}{c + di} \cdot \dfrac{c - di}{c - di} \)
Exemplo: Sejam A = 8 + 5i e B = 7 + 4i.
A/B = \(\dfrac{8 + 5i}{7 + 4i} \cdot \dfrac{7 - 4i}{7 - 4i}\) = \(\dfrac{(8 + 5i)(7 - 4i)}{(7 + 4i)(7 - 4i)}\)
\(\dfrac{(8 + 5i)(7 - 4i)}{(7 + 4i)(7 - 4i)}\) = \(\dfrac{8 \cdot 7 - 8 \cdot 4i + 5i \cdot 7 - 5i \cdot 4i}{7^2 + (4i)^2}\)
\(\dfrac{56 - 32i + 35i - 20i^2}{49 + 16i^2}\) = \(\dfrac{56 + 3i + 20}{49 - 16}\) = \(\dfrac{76 + 3i}{33}\)
Módulo de um número complexo é o comprimento do segmento formado unindo-se a origem do plano cartesiano ao afixo do número complexo. Dado z = a + bi, seu módulo é
|z| = \( \sqrt{a^2 + b^2} \)
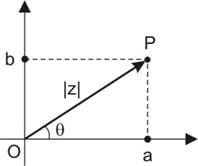
Note que o módulo é a hipotenusa do triângulo retângulo de catetos a e b.
Exemplo:
O módulo de z = 4 + 3i vale:
|z| = \( \sqrt{4^2 + 3^2} \) = \( \sqrt{16 + 9} \) = \( \sqrt{25} \) = 5
Graficamente:

Argumento (θ) de um número complexo é o ângulo formado entre o segmento, obtido pela união entre a origem e o afixo, e o eixo real, orientado positivamente a partir do eixo para o segmento, no sentido anti-horário.

Exemplo:
Para determinar o argumento de z = 1 + i, primeiramente determina-se o módulo:
|z| = \( \sqrt{1^2 + 1^2} \) = \( \sqrt{1 + 1} \) = \( \sqrt{2} \)
Graficamente:

O próximo passo é determinar o argumento θ:
cos θ = \(\dfrac{a}{|z|}\) = \(\dfrac{1}{\sqrt{2}}\) = \(\dfrac{\sqrt{2}}{2}\)
sen θ = \(\dfrac{b}{|z|}\) = \(\dfrac{1}{\sqrt{2}}\) = \(\dfrac{\sqrt{2}}{2}\)
Note que cos θ > 0 e sen θ > 0. Isso significa que θ está no primeiro quadrante.
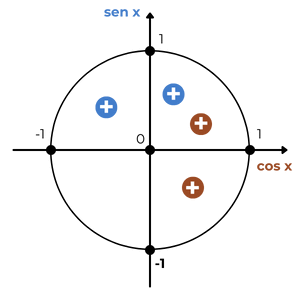
Portanto, θ = 45º.
É possível escrever um complexo z = a + bi (forma algébrica) em função do seu módulo e do seu argumento (forma trigonométrica).
| Forma algébrica | Forma trigonométrica |
|---|---|
| z = a + bi | z = |z| ∙ (cos θ + i ∙ sen θ) |
Exemplo:
Para determinar a forma trigonométrica de z = 2\(\sqrt{2}\) + 2\(\sqrt{2}\)i, primeiramente deve-se calcular o módulo e o argumento de z:
Módulo: |z| = \( \sqrt{(2\sqrt{2})^2 + (2\sqrt{2})^2} \) = \( \sqrt{8 + 8} \) = \( \sqrt{16} \) = 4
Argumento:
cos θ = \(\dfrac{a}{|z|}\) = \(\dfrac{2\sqrt{2}}{4}\) = \(\dfrac{\sqrt{2}}{2}\)
sen θ = \(\dfrac{b}{|z|}\) = \(\dfrac{2\sqrt{2}}{4}\) = \(\dfrac{\sqrt{2}}{2}\)
θ = 45º
Com o valor do módulo e do argumento, o próximo passo é determinar a forma trigonométrica de z:
z = |z| ∙ (cos θ + i ∙ sen θ)
z = 4 ∙ (cos 45º + i ∙ sen 45º)
z\(^n\) = (a + bi)\(^n\)
z\(^n\) = |z|\(^n\) ∙ (cos (n ∙ θ) + i ∙ sen (n ∙ θ))
Exemplo:
Sendo z = 2 ∙ (cos 45º + i ∙ sen 45º), z\(^4\) é calculado da seguinte forma:
z\(^4\) = 2\(^4\) ∙ [cos (4 ∙ 45º) + i ∙ sen (4 ∙ 45º)]
z\(^4\) = 16 ∙ (cos 180º + i ∙ sen 180º)
z\(^4\) = 16 ∙ (-1 + i ∙ 0) = -16
Determine o módulo de z = -12 + 5i.
Solução
|z| = \( \sqrt{(-12)^2 + 5^2} \) = \( \sqrt{144 + 25} \) = \( \sqrt{169} \) = 13
Graficamente:

Determine o argumento de z = 2 - 2\(\sqrt{3}\)i.
Solução
O primeiro passo é determinar o módulo:
|z| = \( \sqrt{2^2 + (2\sqrt{3})^2} \) = \( \sqrt{4 + 12} \) = \( \sqrt{16} \) = 4
Com o módulo determinado, o próximo passo é calcular o argumento:
cos θ = \(\dfrac{a}{|z|}\) = \(\dfrac{2}{4}\) = \(\dfrac{1}{2}\)
sen θ = \(\dfrac{b}{|z|}\) = \(\dfrac{-2\sqrt{3}}{4}\) = -\(\dfrac{\sqrt{3}}{2}\)
Note que cos θ > 0 e sen θ < 0. Isso significa que θ está no quarto quadrante.
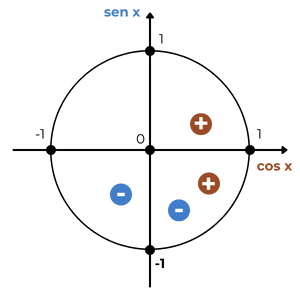
Portanto, θ = 300º
Represente z = 4 - 4\(\sqrt{3}\)i na forma trigonométrica.
Solução
Primeiramente deve-se calcular o módulo e o argumento de z:
Módulo: |z| = \( \sqrt{4^2 + (-4\sqrt{3})^2} \) = \( \sqrt{16 + 48} \) = \( \sqrt{64} \) = 8
Argumento:
cos θ = \(\dfrac{a}{|z|}\) = \(\dfrac{4}{8}\) = \(\dfrac{1}{2}\)
sen θ = \(\dfrac{b}{|z|}\) = \(\dfrac{-4\sqrt{3}}{8}\) = -\(\dfrac{\sqrt{3}}{2}\)
θ = 300º
Com o valor do módulo e do argumento, o próximo passo é determinar a forma trigonométrica de z:
z = |z| ∙ (cos θ + i ∙ sen θ)
z = 8 ∙ (cos 300º + i ∙ sen 300º)
Sendo z = 3 + 4i, calcule o módulo de z\(^4\).
Solução
O módulo de z\(^4\) é:
|z\(^4\)|
|z\(^4\)| é equivalente a (|z|)\(^4\)
Portanto, basta calcular |z| e, após, elevá-lo ao expoente 4.
Módulo: |z| = \( \sqrt{3^2 + 4^2} \) = \( \sqrt{9 + 16} \) = \( \sqrt{25} \) = 5
5\(^4\) = 625
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.