Estudar o sinal de uma função é determinar para quais valores de x ∈ D(f) tem-se:

• f(x) > 0
• f(x) = 0
• f(x) < 0

Em outras palavras, estudar o sinal de uma função é determinar os valores do domínio que fazem com que a imagem da função seja:

• positiva ( f(x) > 0 )
• raiz da função ( f(x) = 0 )
• negativa ( f(x) < 0 )

Entendi

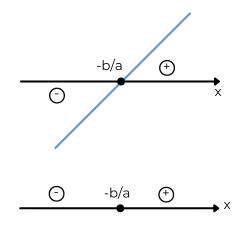
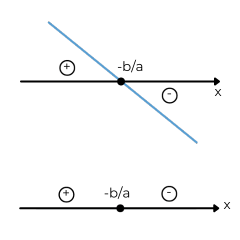
Seja a função do 1º grau f(x) = ax + b.

A raiz dela é dada por:

y = ax + b

0 = ax + b

x = -b/a

O quadro abaixo apresenta o estudo do sinal para y = ax + b.

a > 0	a < 0
f(x) = 0 para x = -b/a Raiz da função f(x) > 0 para x > -b/a A função é positiva quando x é maior que -b/a f(x) < 0 para x < -b/a A função é negativa quando x é menor que -b/a	f(x) = 0 para x = -b/a Raiz da função f(x) > 0 para x < -b/a A função é positiva quando x é menor que -b/a f(x) < 0 para x > -b/a A função é negativa quando x é maior que -b/a

Voltar Entendi

Analise o gráfico e as afirmações abaixo:

• I - f(x) > 3 para x < 3
• II - f(x) > 3 para x > 3
• III - f(x) < 3 para x > 3
• IV - f(x) < 3 para x < 3
• V - f(x) = 0 para x = 3

Podemos afirmar que é(são) verdadeira(s)

I e III II, IV e V I, III e V Todas

Dada a função f(x) = 2x – 4, determine os valores reais de x para os quais:

• a) f(x) > 0
• b) f(x) = 0
• c) f(x) < 0

Solução

Podemos notar que a função é crescente, pois a = 2 > 0.

O zero da função é dado por:

2x – 4 = 0

2x = 4

x = 2

Note que:

• a) f(x) > 0 para x ∈ ]2, ∞[
• b) f(x) = 0 para x = 2
• c) f(x) < 0 para x ∈ ]-∞, 2[

Voltar Entendi

Dada a função f(x) = -2x – 4, determinar os calores reais de x para os quais:

• a) f(x) > 0
• b) f(x) = 0
• c) f(x) < 0

Solução

Podemos notar que a função é decrescente, pois a = -2 < 0.

O zero da função é dado por:

-2x – 4 = 0

-2x = 4

x = -2

Note que:

• a) f(x) > 0 para x ∈ ]-∞, -2[
• b) f(x) = 0 para x = -2
• c) f(x) < 0 para x ∈ ]-2, ∞[

Voltar Entendi

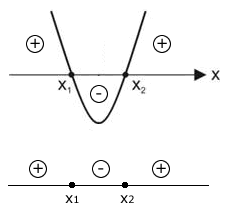
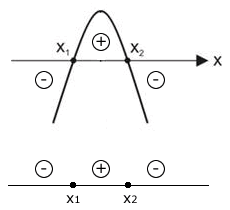
Seja a função do 2º grau definida por f(x) = ax² + bx + c. Os sinais desta função são determinados a partir dos sinais do coeficiente a e do discriminante ∆.

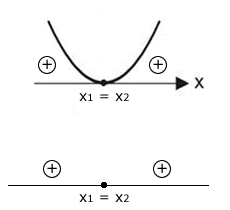
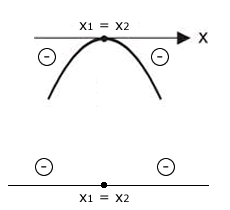
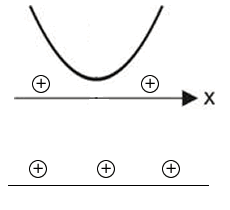
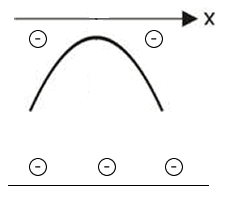
Sejam x\(_1\) e x\(_2\) as raízes de f(x). O quadro abaixo apresenta o estudo do sinal para f(x).

∆	a > 0	a < 0
∆ > 0	f(x) > 0 para x < x\(_1\) ou x > x\(_2\) f(x) = 0 para x = x\(_1\) ou x = x\(_2\) f(x) < 0 para x\(_1\) < x < x\(_2\)	f(x) > 0 para x\(_1\) < x < x\(_2\) f(x) = 0 para x = x\(_1\) ou x = x\(_2\) f(x) < 0 para x < x\(_1\) ou x > x\(_2\)
∆ = 0	f(x) > 0 para x ∈ R | x ≠ -b/2a f(x) = 0 para x = -b/2a f(x) < 0 para nenhum x ∈ R	f(x) > 0 para nenhum x ∈ R f(x) = 0 para x = -b/2a f(x) < 0 para x ∈ R | x ≠ -b/2a
∆ < 0	f(x) > 0 para todo x ∈ R	f(x) < 0 para todo x ∈ R

Voltar Entendi

Dada a função f(x) = 3x² - 4x + 5, determine os valores reais de x para os quais:

• a) f(x) > 0
• b) f(x) = 0
• c) f(x) < 0

Solução

A concavidade da parábola é voltada para cima pois o coeficiente é positivo (3 > 0).

∆ = b² - 4ac = (-4)² - 4 (3) (5) = 16 - 60 = -44 < 0

Como ∆ é negativo, não existem raízes reais.

Assim:

• a) f(x) > 0, ∀x ∈ R
• b) f(x) = 0 para nenhum x ∈ R
• c) f(x) < 0 para nenhum x ∈ R

Voltar Entendi

Dê a variação de sinais da função f(x) = x² - 4x.

Solução

A concavidade da parábola é voltada para cima pois o coeficiente é positivo (1 > 0).

Raízes: x² - 4x = 0

x (x - 4) = 0

x = 0 ou x = 4

Esquematicamente, tem-se:

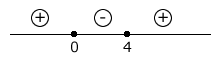
Assim:

• f(x) > 0 para x < 0 ou x > 4
• f(x) = 0 para x = 0 ou x = 4
• f(x) < 0 para 0 < x < 4

Voltar Entendi

Dê a variação de sinais da função f(x) = -x² + 4x - 3.

Solução

A concavidade da parábola é voltada para baixo pois o coeficiente é negativo (-1 < 0).

Raízes:

∆ = b² - 4ac = (4)² - 4 (-1) (-3) = 16 - 12 = 4

x = \(\dfrac{-b \pm \sqrt{\Delta}}{2a}\) = \(\dfrac{-4 \pm \sqrt{4}}{2(-1)}\) = \(\dfrac{-4 \pm 2}{-2}\)

x' = \(\dfrac{-4 + 2}{-2}\) = \(\dfrac{-2}{-2}\) = 1

x" = \(\dfrac{-4 - 2}{-2}\) = \(\dfrac{-6}{-2}\) = 3

Esquematicamente, tem-se:

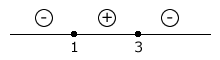
Assim:

• f(x) > 0 para 1 < x < 3
• f(x) = 0 para x = 1 ou x = 3
• f(x) < 0 para x < 1 ou x > 3

Voltar Entendi