

Lembra de funções? Agora iremos conhecer as funções trigonométricas.
Chama-se função seno a função definida por
f: \( \mathbb{R} \) → [-1, 1] tal que f(x) = sen x
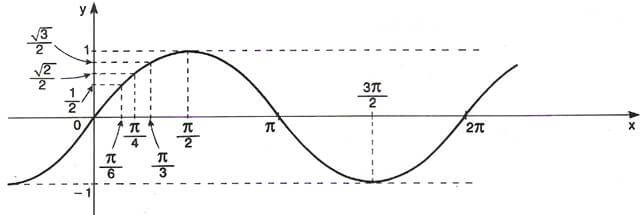
Observe no gráfico que:
PARIDADE, PERÍODO E AMPLITUDE
Paridade: O seno é uma função ímpar, pois ∀x, x ∈ \(\mathbb{R}\), tem-se sen (-x) = - sen x
Período: Observe que sen x = sen (x + 2\(\pi\)), ∀x, x ∈ \(\mathbb{R}\). Logo, a função seno é periódica e seu período vale 2\(\pi\)
Determine k de modo que sen x = 3k + 1.
Solução
Como -1 ≤ sen x ≤ 1, tem-se:
-1 ≤ 3k + 1 ≤ 1
-1 - 1 ≤ 3k ≤ 1 - 1
-2 ≤ 3k ≤ 0
-2/3 ≤ k ≤ 0
Determine o conjunto imagem de y = 1 + sen x.
Solução
A imagem de sen x é [-1, 1]
A imagem de 1 + sen x é [1 - 1, 1 + 1] = [0, 2]
Chama-se função seno a função definida por
f: \( \mathbb{R} \) → [–1, 1] tal que f(x) = cos x
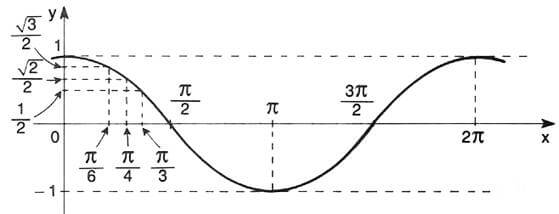
Observe no gráfico que:
PARIDADE, PERÍODO E AMPLITUDE
Paridade: O cosseno é uma função par, pois ∀x, x ∈ \(\mathbb{R}\), tem-se cos (-x) = cos x
Período: Observe que cos x = cos (x + 2\(\pi\)), ∀x, x ∈ \(\mathbb{R}\). Logo, a função cosseno é periódica e seu período vale 2\(\pi\)
Determine k de modo que cos x = \(\dfrac{k - 3}{2}\).
Solução
Como -1 ≤ cos x ≤ 1, tem-se:
-1 ≤ \(\dfrac{k - 3}{2}\) ≤ 1
2 ∙ (-1) ≤ k - 3 ≤ 2 ∙ 1
-2 ≤ k - 3 ≤ 2
-2 + 3 ≤ k ≤ 2 + 3
1 ≤ k ≤ 5
Determine o conjunto imagem de y = 1 + 2 cos x.
Solução
A imagem de cos x é [-1, 1]
A imagem de 2 cos x é [2(-1), 2(1)] = [-2, 2]
A imagem de 1 + 2 cos x é [1 - 2, 1 + 2] = [-1, 3]
Chama-se função tangente a função definida por
f: {x ∈ \( \mathbb{R} \) | x ≠ \( \dfrac{\pi}{2} \) + k π, k ∈ \( \mathbb{Z} \)} → \( \mathbb{R} \) tal que f(x) = tg x
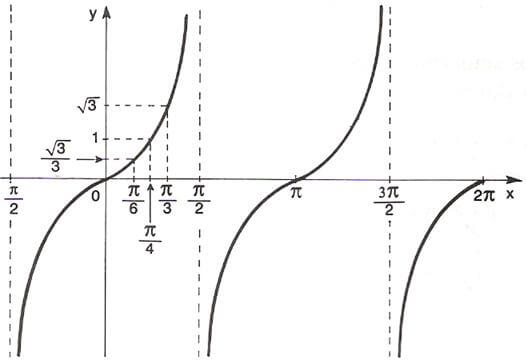
Observe no gráfico que:
PARIDADE, PERÍODO E AMPLITUDE
Paridade: A tangente é uma função ímpar, pois ∀x, x ∈ D, tem-se tg (-x) = - tg x
Período: Observe que tg x = tg (x + \(\pi\)), ∀x, x ∈ D. Logo, a função cosseno é periódica e seu período vale \(\pi\)
Determine o domínio de y = tg \(\left(2x - \dfrac{\pi}{3}\right)\).
Solução
Para tg x, o domínio D(f) = {x ∈ \(\mathbb{R}\) | x ≠ \(\dfrac{\pi}{2}\) + k\(\pi\)}
Logo, para tg \(\left(2x - \dfrac{\pi}{3}\right)\), tem-se:
2x - \(\pi\)/3 ≠ \(\pi\)/2 + k\(\pi\)
2x ≠ \(\pi\)/2 + k\(\pi\) + \(\pi\)/3
2x ≠ 5\(\pi\)/6 + k\(\pi\)
x ≠ 5\(\pi\)/12 + k\(\pi\)/2
D(f) = {x ∈ \(\mathbb{R}\) | x ≠ 5\(\pi\)/12 + k\(\pi\)/2, k ∈ \(\mathbb{Z}\)}
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.