

Para resolver equações trigonométricas, é primordial conhecer praticamente todos os conceitos vistos anteriormente em Trigonometria.
Dominar o ciclo trigonométrico é fundamental para ir bem em Trigonometria. Então, observe com atenção e procure montá-lo em seu caderno para melhor fixação.
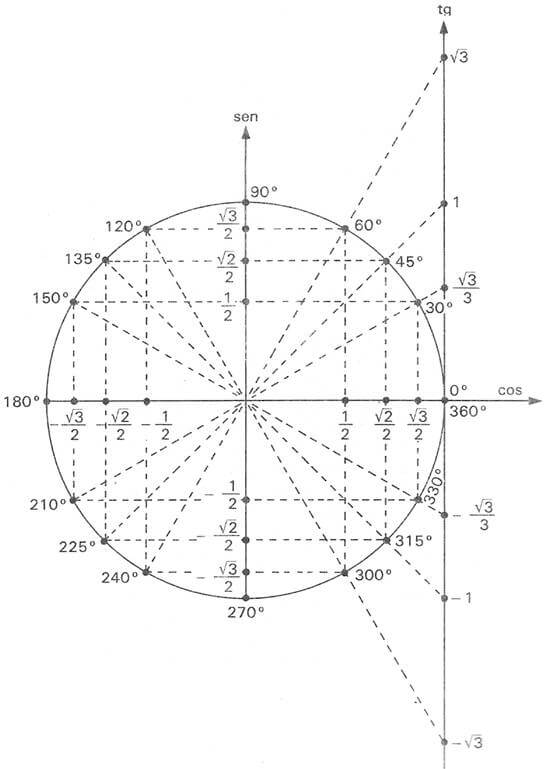
Note que:
Exemplo:
Para determinar seno, cosseno e tangente de 1920º, deve-se primeiramente obter o arco côngruo situado entre 0º e 360º. Para isso, basta dividir 1920º por 360º:
Dividindo 1920º por 360º obtém 5 voltas completas e resto 120º. Esse resto é o arco côngruo situado entre 0º e 360º de 1920º.
Assim:
Resolva a equação cos 3x = 1/2.
Solução
Observando o ciclo trigonométrico, 1/2 = cos 60º = cos 300º = cos -60º = ...
Assim, pode-se escrever:
cos 3x = 1/2
cos 3x = cos 60º = cos 300º = cos -60º = ...
Repare que 3x = 60º = 300º = -60º = ...
Isso significa que 3x deve ser côngruo de 60º. Então:
3x = ±60º + k ∙ 360º (÷3)
x = ±20º + k ∙ 120º, k ∈ \(\mathbb{Z}\)
Resolva a equação sen x + cos x = ±\(\sqrt{2}\).
Solução
Elevando os dois membros ao quadrado:
(sen x + cos x)² = \((\pm\sqrt{2})^2\)
sen²x + 2 ∙ sen x ∙ cos x + cos²x = 2
Como:
Substituindo, vem:
sen²x + 2 ∙ sen x ∙ cos x + cos² = 2 x
1 + sen 2x = 2
sen 2x = 1
Tem-se seno igual a 1 para o arco de 90º ou para os arcos côngruos de 90º. Logo:
2x = 90º + k ∙ 360º
x = 45º + k ∙ 180º, k ∈ \(\mathbb{Z}\)
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.