

Ciclo trigonométrico é uma circunferência de raio igual a 1, na qual se adota um ponto A chamado origem dos arcos e o sentido positivo de percurso como sendo o sentido anti-horário (o sentido horário é o sentido negativo).
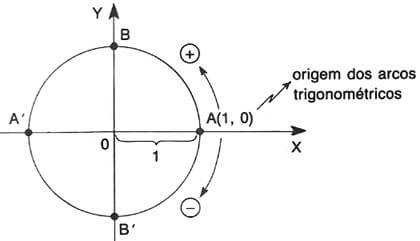
Dividimos o ciclo trigonométrico em quatro partes utilizando dois eixos perpendiculares entre si, ambos passando pelo centro do ciclo e um deles passando pelo ponto origem A. Estes eixos perpendiculares formam o plano cartesiano.
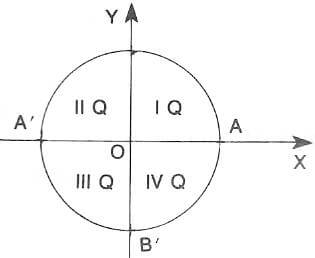
Chamamos de quadrantes a cada uma dessas quatro partes em que ficou dividido o ciclo.
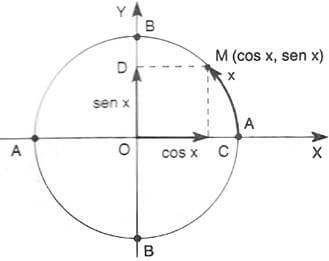
O eixo das abscissas é o eixo dos cossenos e o das ordenadas é o dos senos.
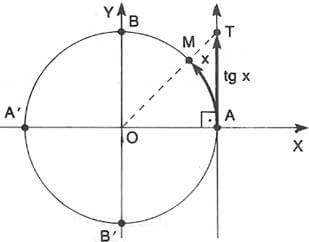
O eixo das tangentes é o eixo paralelo ao das ordenadas e que passa pelo ponto A.

Os ângulos de 135º e 299º estão, respectivamente, nos quadrantes
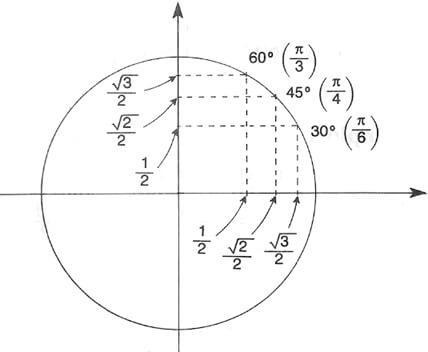
Ângulos notáveis são aqueles mais conhecidos conforme apresenta a tabela.
| ÂNGULO | 0º | 30º | 45º | 60º | 90º |
| 0 rad | \( \dfrac{\pi}{6} \) rad | \( \dfrac{\pi}{4} \) rad | \( \dfrac{\pi}{3} \) rad | \( \dfrac{\pi}{2} \) rad | |
| Seno | 0 | \( \dfrac{1}{2} \) | \( \dfrac{\sqrt{2}}{2} \) | \( \dfrac{\sqrt{3}}{2} \) | 1 |
| Cosseno | 1 | \( \dfrac{\sqrt{3}}{2} \) | \( \dfrac{\sqrt{2}}{2} \) | \( \dfrac{1}{2} \) | 0 |
| Tangente | 0 | \( \dfrac{\sqrt{3}}{3} \) | 1 | \( \sqrt{3} \) | não existe |
| Seno é maior que 0 nos quadrantes I e II | 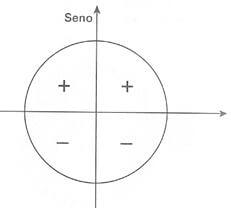 |
| Cosseno é maior que 0 nos quadrantes I e IV | 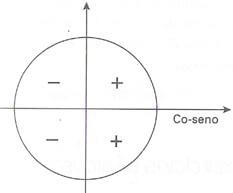 |
| Tangente é maior que 0 nos quadrantes I e III | 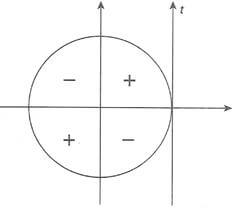 |

Em quais quadrantes o seno é positivo?

Seno, cosseno e tangente são positivos no

Se α é um ângulo do II Q, então (sen α)(cos α)(tg α) é
Determine o quadrante a que pertence o arco de 72º.
Solução
Ora, 72º está entre 0 e 90º. Logo, 72º ∈ IQ
Determine o quadrante a que pertence o arco de 235º.
Solução
Ora, 235º está entre 180º e 270º. Logo, 235º ∈ IIIQ
Determine o quadrante a que pertence o arco de -200º.
Solução
Para determinar a extremidade de -200º, basta percorrer o ciclo trigonométrico 200º no sentido negativo, ou seja, no sentido horário.
Pode ainda, obter o arco côngruo de -200º na primeira volta positiva:
-200º + 360º = 160º
Como 160º está entre 90º e 180º, 160º ∈ IIQ. Logo, -200º ∈ IIQ
Determine o quadrante a que pertence o arco de 3π/4.
Solução
3π/4 está entre π/2 e π. Logo, 3π/4 ∈ IIQ
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.