Dois arcos trigonométricos são côngruos se, e somente se, suas extremidades coincidem.

No ciclo, repare que os ângulos 0º, 360º e 720º são côngruos.

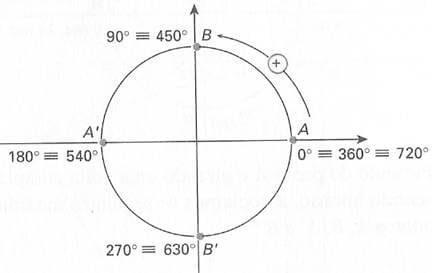
Em radianos, o mesmo acontence: 0, 2π e 4π são côngruos.

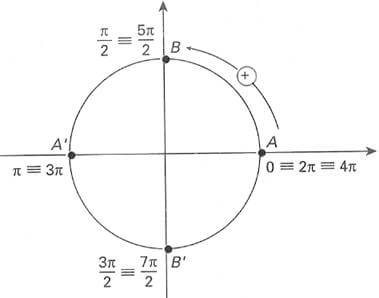
Exemplo:

Os arcos 40º e 400º são coincidentes, ou seja, terminam num mesmo ponto.

• 40º = 40º + 0º
• 400º = 40º + 360º

Note, ainda, que há outros arcos que coincidem com 40º:

• 760º = 40º + 720º
• -320º = 40º - 360º
• -680º = 40º - 720º

Estes arcos são côngruos e podem ser determinados pela seguinte expressão:

x = 40º + k ∙ 360º, k ∈ \(\mathbb{Z}\)

Entendi

Observe as simetrias entre os arcos no ciclo abaixo, sendo α uma medida em graus.

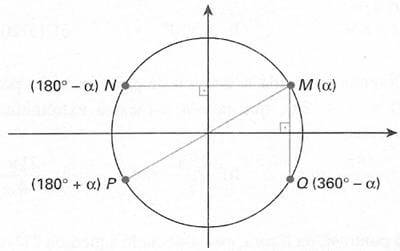
O próximo ciclo apresenta as simetrias, considerando α uma medida em radianos.

Voltar Entendi

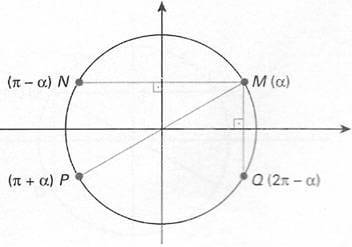
Determine o quadrante em que se encontra a extremidade do arco 1 280º.

Solução

Dividindo 1 280º por 360º, obtém-se como quociente 3 e resto 200º. Isso significa que o arco percorre 3 voltas completas no ciclo mais 200º.

Logo, 1 280º é congruente (côngruo) de 200º, ou seja, possuem mesma extremidade.

Observando o ciclo trigonométrico, 200º está entre 180º e 270º. Assim, 1 280º está no 3º quadrante

Voltar Entendi

Determine os arcos côngruos de π.

Solução

Percorrendo o ciclo trigonométrico pelo sentido positivo, tem-se:

• 1ª volta: π = π + 0 ∙ 2 π
• 2ª volta: π + 2 ∙ π = π + 1 ∙ 2 π
• 3ª volta: π + 4 ∙ π = π + 2 ∙ 2 π
• 4ª volta: π + 6 ∙ π = π + 3 ∙ 2 π
• E assim por diante

Os arcos côngruos de π podem ser expressos como x = π + k ∙ 2 π, k ∈ \(\mathbb{Z}\)

Voltar Entendi