

Chama-se prisma ao poliedro convexo tal que duas faces são polígonos convexos congruentes situadas em planos paralelos e as demais faces são paralelogramos.
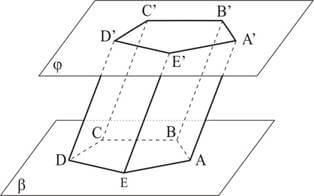
Elementos:
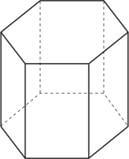
O prisma recebe o nome de acordo com o número de lados de um dos polígonos das bases.
Secção transversal
Chama-se secção transversal de um prisma a uma secção paralela às bases desse prisma.
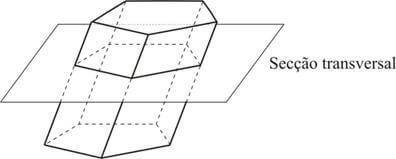
Propriedade: Toda secção transversal de um prisma é congruente às bases.
Prisma reto: é aquele cujas arestas laterais são perpendiculares aos planos das bases. As faces laterais são retângulos.
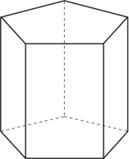
Prisma oblíquo: é aquele cujas arestas laterais são oblíquas aos planos das bases.
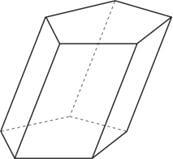
Prisma regular é um prisma reto cujas bases são polígonos regulares. As faces laterais são retângulos congruentes entre si.
Assim, no prisma triangular regular, as bases são triângulos equiláteros, no prisma quadrangular regular, as bases são quadrados, e assim por diante.
A área lateral de um prisma é a área de sua superfície lateral.
A área total de um prisma é a área de sua superfície total.
S\(_T\) = 2 ∙ S\(_B\) + S\(_L\)
O volume de um prisma é dado por
V = S\(_B\) ∙ H
Paralelepípedo é o prisma cujas bases são paralelogramos.

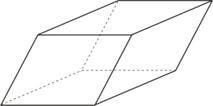
Chama-se paralelepípedo reto-retângulo ao prisma reto de bases retangulares.
Chama-se cubo ao paralelepípedo reto-retângulo que tem todas as arestas congruentes entre si. As faces do cubo são quadrados congruentes entre si.
A área lateral de um paralelepípedo é a área de sua superfície lateral.
A área total de um paralelepípedo é a área de sua superfície total.
ST = 2 ∙ S\(_B\) + S\(_L\)
S\(_T\) = 2 ∙ (a ∙ b + a ∙ c + b ∙ c)
O volume de um paralelepípedo é dado por
V = S\(_B\) ∙ H
V = a ∙ b ∙ c
As dimensões de um paralelepípedo retângulo são 5m, 4m e 3m. Determine o volume, a área e a diagonal desse sólido.
Solução
Sejam a = 5, b = 4 e c = 3.
O volume é igual ao produto das três medidas:
V = a ∙ b ∙ c = 5 ∙ 4 ∙ 3 = 60 m\(^3\)
A área é dada pela soma das áreas laterais:
S = 2 (ab + ac + bc) = 2 (5 ∙ 4 + 5 ∙ 3 + 4 ∙ 3) = 2 (20 + 15 + 12) = 2 (47) = 94 m²
A diagonal é dada por:
D = \(\sqrt{a^2 + b^2 + c^2}\) = \(\sqrt{5^2 + 4^2 + 3^2}\) = \(\sqrt{25 + 16 + 9}\) = \(\sqrt{50}\) = 5\(\sqrt{2}\) m
As dimensões a, b e c de um paralelepípedo retângulo são proporcionais a 2, 3 e 5, respectivamente. Sabendo que o volume desse sólido é 810 cm³, determine a, b e c.
Solução
Segundo o enunciado, tem-se:
\(\dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{5} = k\)
Logo:
Como o volume vale 810 cm³, tem-se:
V = a ∙ b ∙ c
810 = 2k ∙ 3k ∙ 5k
810 = 30k³
k³ = 27
k = 3
Substituindo, vem:
a = 2k = 2(3) = 6 cm
b = 3k = 3(3) = 9 cm
c = 5k = 5(3) = 15 cm
Determine a área total de um cubo sabendo que a medida de uma de suas diagonais excede de \(\sqrt{2}\) a medida de uma diagonal da face.
Solução
Sejam d e D as diagonais de uma face e do cubo de aresta x, respectivamente. As diagonais são dadas por:
Segundo o enunciado, tem-se:
D = d + \(\sqrt{2}\) ⇔ x\(\sqrt{3}\) = x\(\sqrt{2}\) + \(\sqrt{2}\) ⇔ x\(\sqrt{3}\) - x\(\sqrt{2}\) = \(\sqrt{2}\)
x (\(\sqrt{3}\) - \(\sqrt{2}\)) = \(\sqrt{2}\) ⇔ x = \(\dfrac{\sqrt{2}}{\sqrt{3} - \sqrt{2}}\)
Racionalizando, vem:
x = \(\dfrac{\sqrt{2}}{\sqrt{3} - \sqrt{2}} \cdot \dfrac{\sqrt{3} + \sqrt{2}}{\sqrt{3} + \sqrt{2}}\) = \(\sqrt{6}\) + 2
Como a área total é igual a seis vezes a área de uma face, vem:
S = 6x² = 6 \((\sqrt{6} + 2)^2\) = 6 (6 + 4\sqrt{6} + 4) = 12 (5 + 2\(\sqrt{6}\)) cm²
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.