

Cone reto (ou cone circular reto ou cone de revolução) é um sólido gerado pela rotação completa de um triângulo retângulo em torno de um de seus catetos.
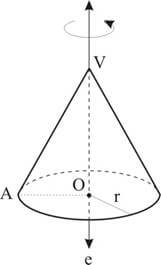
Em outras palavras, é limitado por uma base circular e uma superfície afunilada que é sua superfície lateral. Chamamos de geratriz g do cone ao segmento que une o vértice a qualquer ponto da superfície da base e de altura h a distância do vértice V ao plano da base do cone.
Elementos:
Secção transversal é a intersecção dele com um plano paralelo à base e que não contém o vértice.
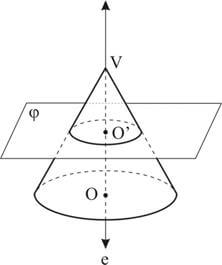
Toda secção transversal de um cone de revolução é semelhante à base.
Secção meridiana é a intersecção do cone com um plano que contém seu eixo.
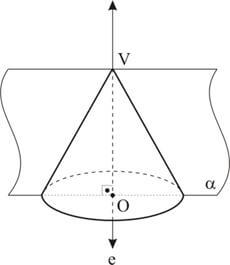
Toda secção meridiana de um cone de revolução é um triângulo isósceles.
Superfície lateral: é a união de suas geratrizes. A área lateral é equivalente a um setor circular.
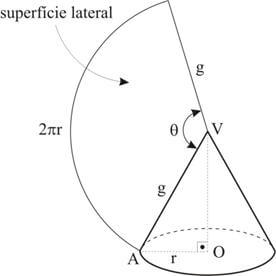
Superfície total: é a união da superfície lateral com a sua base.
Chama-se equilátero ao cone que a geratriz é igual ao diâmetro da base, portanto o cone equilátero g = 2r.
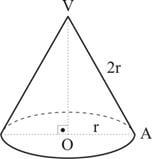
Toda secção meridiana de um cone equilátero é um triângulo equilátero.
A área lateral de um cone é a área de sua superfície lateral.
S\(_L\) = π ∙ r ∙ g
A área total de um cone é a soma da área lateral com a área da base.
S\(_T\) = S\(_L\) + S\(_B\)
S\(_T\) = π ∙ R ∙ (g + R)
O volume de um cone é dado por
V = \( \dfrac{1}{3} \cdot S_B \cdot H \)
V = \( \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot H \)
Num cone reto, a altura e a geratriz medem 4 m e 5 m, respectivamente. Determine o volume e a área desse cone.
Solução
\(g^2 = r^2 + h^2\)
5² = r² + 4²
r² = 25 - 16
r = 3
Área da base:
B = π ∙ r²
B = π ∙ 3² = 9π m²
Volume:
V = \( \dfrac{1}{3} \cdot B \cdot h \) = \( \dfrac{1}{3} \cdot 9\pi \cdot 4 \) = 12π m³
Determine o volume e a área da secção meridiana de um cone equilátero cuja área da superfície mede 48π cm².
Solução
No cone equilátero a geratriz é igual ao diâmetro da base: g = d = 2r
A área da superfície é dada por S = π ∙ r ∙ (g + r)
Substituindo g = 2r, vem:
S = π ∙ r ∙ (g + r) = π ∙ r ∙ (2r + r) = 3πr²
Segundo o enunciado, S = 48π cm²
Então:
48π = 3πr²
r² = 16
r = 4
O próximo passo é calcular a altura do cone. Como o cone é equilátero, sua altura é igual à altura do triângulo equilátero de lado g. Como g = 2r e r = 4, tem-se:
g = 2r = 2(4) = 8
Altura do triângulo equilátero:
h = \(\dfrac{g \cdot \sqrt{3}}{2}\) = \(\dfrac{8 \cdot \sqrt{3}}{2}\) = 4\(\sqrt{3}\)
Volume:
V = \(\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h \) = \(\dfrac{1}{3} \cdot \pi \cdot 4^2 \cdot 4\sqrt{3} \) = \(\dfrac{64\pi\sqrt{3}}{3}\) cm³
Área da secção meridiana (Ss):
A secção meridiana é o triângulo equilátero de lado g = 8 e h = 4\(\sqrt{3}\)
Logo, a área do triângulo equilátero é dada por:
Ss = \(\dfrac{g \cdot h}{2}\) = \(\dfrac{8 \cdot 4\sqrt{3}}{2}\) = 16\(\sqrt{3}\) cm²
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.