

O cilindro reto (ou cilindro circular reto ou cilindro de revolução) é limitado por dois círculos paralelos de mesmo raio, que são suas bases e uma superfície arredondada que é a superfície lateral do cilindro. A reta que une os centros dos dois círculos chama-se eixo do cilindro.
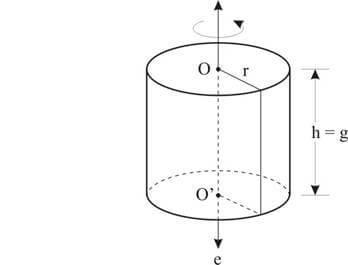
Elementos:
Secção transversal é a intersecção do cilindro com um plano paralelo às bases.
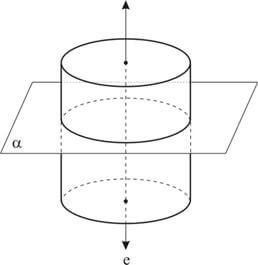
Propriedade: Toda secção transversal de um cilindro de revolução é congruente às bases desse cilindro.
Secção meridiana é a intersecção do cilindro com um plano que contém seu eixo.
Propriedade: Toda secção meridiana de um cilindro de revolução é um retângulo.
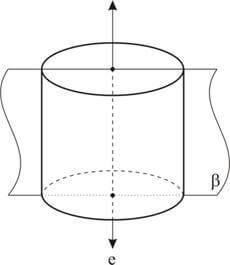
Secção paralela ao eixo do cilindro é a secção que se obtém cortando o cilindro com um plano paralelo ao eixo do mesmo.
Chama-se cilindro equilátero ao cilindro reto em que a altura é igual ao diâmetro da base, portanto o cilindro equilátero h = 2 ∙ r.
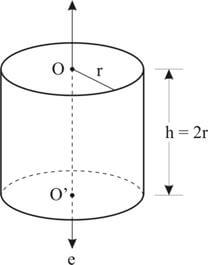
Propriedade: Toda secção meridiana de um cilindro equilátero é um quadrado.
A área lateral de um cilindro é a área da superfície lateral, ou seja, é o produto do comprimento da circunferência da base pela medida da altura.
S\(_L\) = 2 ∙ π ∙ r ∙ h
A área total de um cilindro é a soma da área lateral com as duas áreas das bases.
\( S_T = 2 \cdot S_B + S_L \)
O volume de um cilindro é dado por
V = π ∙ r² ∙ H
Determine a área e o volume de um cilindro reto cuja altura mede 6 cm e raio da base, 2 cm.
Solução
A área (S) é a soma das áreas das duas bases (2B) com a área lateral (L):
S = 2B + L
Área da base:
B = π ∙ r²
B = π ∙ 2²
B = 4π cm²
Área lateral:
L = 2 ∙ π ∙ r ∙ h
L = 2 ∙ π ∙ 2 ∙ 6
L = 24π cm²
Substituindo, vem:
S = 2B + L
S = 2 (4π) + 24π
S = 8π + 24π = 32π cm²
O volume é determinado por:
V = π ∙ r² ∙ h
V = π ∙ 2² ∙ 6
V = π ∙ 4 ∙ 6 = 24π cm³
Determine a área lateral de um cilindro equilátero cujo volume é 128π cm³.
Solução
A área lateral é dada por S\(_L\) = 2πrh
Como o cilindro é equilátero, a altura é igual ao dobro do raio da base: h = 2r
V = π ∙ r² ∙ h
128π = π ∙ r² ∙ 2r
128π = 2 ∙ π ∙ r³
r³ = 64
r = 4
Substituindo r = 4 em h = 2r, vem:
h = 2 (4) = 8
Calculando a área lateral:
S\(_L\) = 2 ∙ π ∙ r ∙ h = 2 π (4) (8) = 64π cm²
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.