

Considere a seguinte distribuição de frequência:
| Número de acidentes por dia, em 1 mês | Frequências |
|---|---|
| 0 | 22 |
| 1 | 5 |
| 2 | 2 |
| 3 | 1 |
| Total | 30 |
Através dos dados apresentados pode-se calcular a probabilidade de em um dia:
Podemos então elaborar uma tabela denominada distribuição de probabilidade:
| Número de acidentes por dia, em 1 mês | Probabilidade |
|---|---|
| 0 | 0,73 |
| 1 | 0,17 |
| 2 | 0,07 |
| 3 | 0,03 |
| Total | 1,00 |
Podemos definir uma função que associe a variável acidentes com a sua probabilidade. Essa função é chamada de função probabilidade e é definida por:
F(x) = P (X = \(x_i\))
Observe a tabela que indica a quantidade de bolas dentro de uma caixa:
| Cor da bola | Qtd |
|---|---|
| Amarela | 12 |
| Vermelha | 4 |
| Verde | 16 |
| Azul | 8 |
Ao tirar uma bola da caixa sem ver, a probabilidade de tirar uma bola vermelha é de
Entre as distribuições de variável contínua, a distribuição normal é a mais empregada em estatística, considerando a questão prática e teórica. Ela apresenta-se em formato de sino, unimodal, simétrica em relação a sua média e tem como características fundamentais a média (\( \bar{x} \)) e o desvio padrão (s).
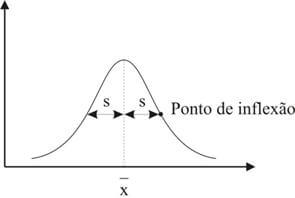
Quando nos referimos a uma distribuição normal, cita-se a média e o seu desvio padrão: N(\( \bar{x} \), s)
A equação da curva é a seguinte:
Y = \( \dfrac{1}{s \sqrt{2\pi}} e^{-\dfrac{1}{2} \left( \dfrac{X - \bar{x}}{s} \right)^2} \)
Quando se tem em mão uma variável aleatória com distribuição normal, o principal interesse é obter a probabilidade de essa variável aleatória assumir um valor em um determinado intervalo. Essa probabilidade é representada pela área sob a curva dentro desse intervalo. A área total sob a curva é 1 (100%). Portanto, a probabilidade de uma observação assumir um valor entre dois pontos quaisquer é igual à área compreendida entre esses dois pontos.
Quanto maior a variablidade dos dados em relação à média, maior a probabilidade de encontrarmos o valor que buscamos embaixo da normal.
Propriedades:
P1. f(x) é simétrica em relação à origem, x = média = 0.
P2. f(x) possui um máximo para z = 0.
P3. f(x) tende a zero quando x tende para + infinito ou - infinito.
P4. f(x) tem dois pontos de inflexão cujas abscissas valem média + DP e média - DP, ou quando z tem dois pontos de inflexão cujas abscissas valem +1 e -1.
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.