

Um polígono regular é inscrito numa circunferência quando todos os seus vértices pertencem a essa circunferência.
Na figura abaixo temos um triângulo inscrito em uma circunferência. Note que seus vértices A, B e C pertencem à circunferência.
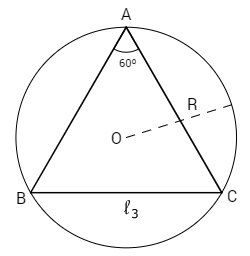
Apótema: Em todo polígono regular, o segmento que une o centro do polígono ao ponto médio de qualquer um dos lados é perpendicular a esse lado e chama-se apótema do polígono regular.
Na figura abaixo temos um quadrado inscrito em uma circunferência. Note que seus vértices A, B, C e D pertencem à circunferência.
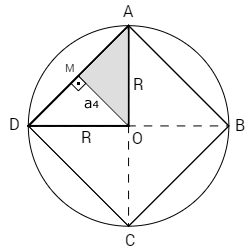
O apótema (a\(_4\)) é o segmento que une o centro do quadrado (O) com o ponto médio (M) de um de seus lados (neste caso, M é o ponto médio do lado AD).
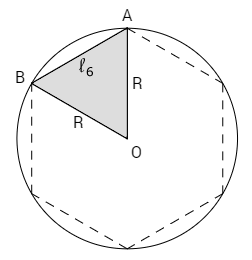
Na figura acima temos um hexágono regular inscrito em uma circunferência. O apótema é o(a)
Para um polígono regular de n lados, considere:
Utilizando essa convenção, será apresentado os cálculos de \(l_n\) e \(a_n\) em função do raio da circunferência circunscrita (R).
Considere um triângulo equilátero inscrito em uma circunferência, conforme ilustra a figura:
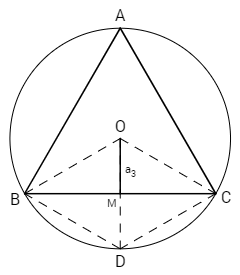
Altura (h):
AO = R ⇔ R = 2h/3
h = 3R/2
Apótema (\(a_3\)):
OM = \(a_3\) = AO/2
\(a_3\) = R/2
Lado (\(l_3\)):
Como h = 3R/2 e h = \(l_3 \cdot \sqrt{3}\)/2 (altura do triângulo equilátero), vem:
3R/2 = \(l_3 \cdot \sqrt{3}\)/2
\(l_3\) = R \(\sqrt{3}\)
O lado pode ser obtido também pela lei dos senos:

\(\dfrac{BC}{sen 60º} = 2R\)
BC = 2 ∙ R ∙ sen 60º
BC = 2 ∙ R ∙ \(\dfrac{\sqrt{3}}{2}\)
BC = R \(\sqrt{3}\)
Considere um quadrado inscrito em uma circunferência, conforme ilustra a figura:
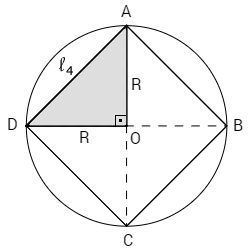
Lado (\(l_4\)): Aplicando o teorema de Pitágoras no triângulo AOB, vem:
\((l_4)^2 = R^2 + R^2\)
\((l_4)^2 = 2R^2\)
\(l_4 = R\sqrt{2}\)

Apótema (\(a_4\)):
Repare que o triângulo AOM é retângulo e isósceles. Como AM = OM pode-se aplicar o teorema de Pitágoras ou proceder da seguinte forma:
OM = \(\dfrac{AB}{2}\)
OM = \(\dfrac{l_4}{2}\)
OM = \(\dfrac{R\sqrt{2}}{2}\)
Considere um hexágono regular inscrito em uma circunferência, conforme ilustra a figura:

Lado (\(l_6\)):
Note que o hexágono regular pode ser dividido em 6 triângulos equiláteros.
Logo, \(l_6\) = R
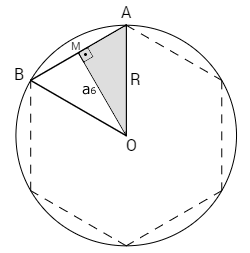
Apótema (\(a_6\)):
Aplicando o teorema de Pitágoras no ∆AMO, vem:
\(R^2 = (a_6)^2 + AM^2\)
AM = \(\dfrac{l_6}{2}\) = R/2
Substituindo, vem:
\(R^2 = (a_6)^2 + \left(\dfrac{R}{2}\right)^2\)
\(R^2 = (a_6)^2 + \dfrac{R^2}{4}\)
\(R^2 - \dfrac{R^2}{4} = (a_6)^2\)
\(\dfrac{3R^2}{4} = (a_6)^2\)
\(a_6 = \dfrac{R\sqrt{3}}{2}\)
Foram apresentadas as relações métricas de alguns polígonos regulares inscritos. Note que o processo para obter as relações métricas são semelhantes. Assim, se você entendeu o processo, está apto a encontrar as relações métricas de outros polígonos regulares sem a necessidade de memorização das fórmulas. Inclusive, caso não lembre das fórmulas apresentadas aqui, basta realizar os procedimentos vistos.
Determine as medidas de um lado e de um apótema de um octógono regular inscrito numa circunferência de centro O e raio R, em função de R.
Como sugestão, o lado pode ser obtido pela lei dos cossenos e o apótema pelo teorema de Pitágoras.
Resposta:
lado → \(l_8 = R\sqrt{2 - \sqrt{2}}\)
apótema → \(a_8 = \dfrac{R}{2}\sqrt{2 + \sqrt{2}}\)
Um hexágono regular com 36 cm de perímetro está inscrito numa circunferência. Determine a medida de um lado e de um apótema de um quadrado inscrito nessa circunferência.
Solução
O primeiro passo é determinar a medida do raio da circunferência.
O hexágono tem 6 lados. Logo, cada lado vale:
\(l_6\) = 36/6 = 6 cm
Como o lado do hexágono regular é igual ao raio da circunferência circunscrita, R = 6.
Com a medida do raio encontrada, o próximo passo é calcular a medida de um lado e de um apótema do quadrado inscrito.
O lado do quadrado inscrito mede:
\(l_4\) = R\(\sqrt{2}\) = 6\(\sqrt{2}\) cm
A apótema do quadrado inscrito mede:
\(a_4\) = R\(\sqrt{2}\)/2 = 6\(\sqrt{2}\)/2 = 3\(\sqrt{2}\) cm
Calcule a medida de um lado e de um apótema de um triângulo equilátero em cuja circunferência circunscrita está inscrito um quadrado de diagonal \(\sqrt{12}\) cm.
Solução
O primeiro passo é determinar a medida do raio da circunferência.
Como a diagonal do quadrado é dada por d = l\(\sqrt{2}\), tem-se:
l\(\sqrt{2}\) = \(\sqrt{12}\)
l = \(\sqrt{6}\)
Como o lado do quadrado inscrito mede \(l_4\) = R\(\sqrt{2}\), tem-se:
\(l_4\) = R\(\sqrt{2}\)
\(\sqrt{6}\) = R\(\sqrt{2}\)
R = \(\sqrt{3}\)
Com a medida do raio encontrada, o próximo passo é calcular a medida de um lado e de um apótema do triângulo inscrito.
\(l_3\) = R\(\sqrt{3}\) = \(\sqrt{3} \cdot \sqrt{3}\) = 3 cm
\(a_3\) = R/2 = \(\sqrt{3}\)/2 cm
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.