Inequações logarítmicas são as inequações que envolvem logaritmos.

Para reolvê-las, temos o seguinte:

• se a base for maior que 1, a relação de desigualdade entre os logaritmos se mantém para os logaritmandos.
• se a base for positivo e menor que 1, a relação de desigualdade entre os logaritmos se inverte para os logaritmandos.

Entendi

Determine os valores de x na inequação \(log_2(2x - 4) < log_2(3x - 9)\)

Solução

Condição de existência:

• (I): 2x - 4 > 0 ⇔ x > 2
• (II): 3x - 9 > 0 ⇔ x > 3

Fazendo (I) ∩ (II), vem:

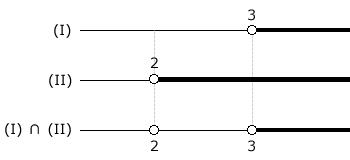
x > 3 (III)

\(log_2(2x - 4) < log_2(3x - 9)\)

2x - 4 < 3x - 9

x > 5 (IV)

Fazendo (III) ∩ (IV), vem:

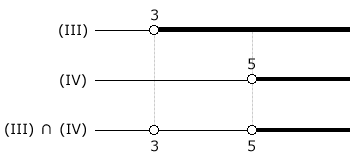
S = ]5, ∞[

Voltar Entendi