

Nesta aula será abordada as leis dos senos e dos cossenos, que podem ser aplicadas em qualquer triângulo.
Em todo triângulo, a medida de cada lado é proporcional ao seno do ângulo oposto a esse lado. A razão da proporção é igual ao dobro do raio da circunferência circunscrita ao triângulo.
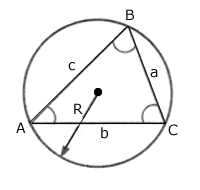
\(\dfrac{a}{sen A} = \dfrac{b}{sen B} = \dfrac{c}{sen C}\) = 2R
Em todo triângulo, o quadrado da medida de qualquer lado é igual à soma dos quadrados das medidas dos outros dois lados menos o dobro do produto das medidas desses dois lados pelo cosseno do ângulo formado por eles.
Para resolução de exercícios de trigonometria de triângulos, são válidas as seguintes regras:
Como há triângulos obtusos, é necessário saber sobre seno e cosseno de ângulo obtuso (90º < x < 180º).
Caso o ângulo seja obtuso, teremos as seguintes regras:
I) O seno de um ângulo obtuso x é igual ao seno do seu suplemento (180º - x):
sen x = sen (180º - x)
II) O cosseno de um ângulo obtuso x é igual ao oposto do cosseno do seu suplemento (180º - x):
cos x = - cos (180º - x)
Essas regras vem do ciclo trigonométrico.
Exemplos:
Num triângulo ABC, os lados AB e AC medem 10cm e 12cm, respectivamente, e o ângulo formado por eles mede 60º. Calcule o lado BC.
Solução
Note que foram dados dois lados e o ângulo formado por eles. Deve-se utizar a lei dos cossenos.
Aplicando a lei dos cossenos, tem-se:
x² = 10² + 12² - 2 ∙ 10 ∙ 12 ∙ cos 60º = 100 + 144 + 240 ∙ (-0,5) = 124
x = \(\sqrt{124}\) = 2\(\sqrt{31}\) cm
Determine o valor de x na figura abaixo sabendo que o ângulo A mede 120º e B mede 45º.
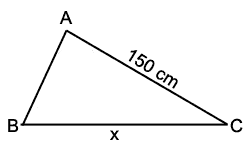
Solução
Note que foram dados dois ângulos e um lado oposto à um dos ângulos. Logo, deve-se utizar a lei dos senos.
Aplicando a lei dos senos, tem-se:
\(\dfrac{BC}{sen A} = \dfrac{AC}{sen B} ⇔ \(\dfrac{x}{sen 120º} = \dfrac{150}{sen 45º}
x ∙ sen 45º = 150 ∙ sen 120º ⇔ x ∙ \(\dfrac{\sqrt{2}}{2}\) = 150 ∙ \(\dfrac{\sqrt{3}}{2}\)
x = 150 ∙ \(\dfrac{\sqrt{3}}{2\sqrt{2}}\) = 150 ∙ \(\dfrac{\sqrt{3}}{2\sqrt{2}}\) ∙ \(\dfrac{\sqrt{2}}{\sqrt{2}}\)
x = 150 ∙ \(\dfrac{\sqrt{6}}{4}\) = \(\dfrac{75 \sqrt{6}}{2}\) cm
Determine o valor de x na figura abaixo.
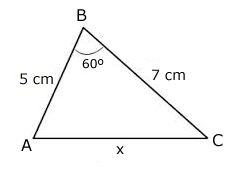
Solução
Note que tem dois lados e o ângulo formado por eles. Logo, deve-se utizar a lei dos cossenos.
Aplicando a lei dos cossenos, tem-se:
x² = 5² + 7² - 2 ∙ 5 ∙ 7 ∙ cos 60º = 25 + 49 - 35 = 39
x = \(\sqrt{39}\) cm
Determine o valor de x na figura abaixo.
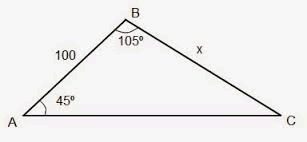
Solução
Note que tem dois ângulos e um lado. Logo, deve-se utizar a lei dos senos.
Como a soma dos ângulos internos de um triângulo é 180º, tem-se que:
105º + 45º + C = 180º ⇔ C = 180º - 150º = 30º
Aplicando a lei dos senos, tem-se:
\(\dfrac{100}{sen 30º} = \dfrac{x}{sen 45º}\) ⇔ 100 ∙ sen 45º = x ∙ sen 30º
100 ∙ \(\dfrac{\sqrt{2}}{2}\) = x ∙ \(\dfrac{1}{2}\) ⇔ x = 100 \(\sqrt{2}\)
Um triângulo ABC está inscrito numa circunferência de raio 12 cm. Calcule o lado BC, sabendo que o ângulo interno  mede 30º.
Solução
O lado BC é oposto ao ângulo de vértice A.
Aplicando a lei dos senos, tem-se:
\(\dfrac{BC}{sen 30º}\) = 2 ∙ 12 ⇔ BC = 2 ∙ 12 ∙ 1/2 = 12 cm
No triângulo ABC da figura, calcule o ângulo  sabendo que a = 2b.
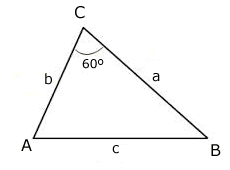
Solução
Aplicando a lei dos cossenos, tem-se:
c² = a² + b² - 2 ∙ a ∙ b ∙ cos 60º
Substituindo a = 2b e cos 60º = 1/2, vem:
c² = (2b)² + b² - 2 ∙ (2b) ∙ b ∙ 1/2
c² = 4b² + b² - 2b²
c² = 3b² ⇔ c = b\(\sqrt{3}\)
Aplicando a lei dos senos, tem-se:
\(\dfrac{c}{sen 60º} = \dfrac{a}{sen Â}\) ⇔ c ∙ sen  = a ∙ sen 60º
b\(\sqrt{3}\) ∙ sen  = 2b ∙ \(\dfrac{\sqrt{3}}{2}\) ⇔ sen  = 1
 = arcsen 1 = 90º
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.