

Consideremos um feixe de retas paralelas a, b, c e duas retas transversais r e s.
As retas paralelas cortam as retas transversais, formando os segmentos \( \overline{AB} \), \( \overline{BC} \), \( \overline{MN} \) e \( \overline{NP} \).
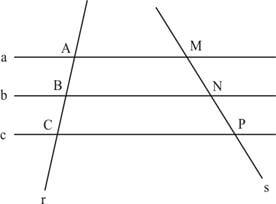
Os segmentos situados sobre as transversais, entre as mesmas paralelas, são chamados de segmentos correspondentes. Assim, na figura, os segmentos correspondentes são: \( \overline{AB} \) e \( \overline{MN} \), \( \overline{BC} \) e \( \overline{NP} \), \( \overline{AC} \) e \( \overline{MP} \).
Um feixe de retas paralelas determina, sobre duas retas transversais, segmentos correspondentes que são proporcionais.
\( \dfrac{AB}{MN} = \dfrac{BC}{NP} = \dfrac{AC}{MP} \)
Determine x e y na figura seguinte, sabendo que r // s // t e que AB = 30.
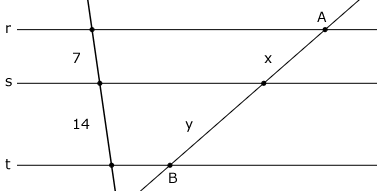
Solução
Pelo teorema de Tales, tem-se:
\(\dfrac{7}{x} = \dfrac{14}{y}\)
7y = 14x
y = 2x (I)
Como AB = 30, então:
AB = 30
x + y = 30 (II)
Substituindo (I) em (II), vem:
x + (2x) = 30
3x = 30
x = 10
Substituindo x = 10 em (I), vem:
y = 2 (10) = 20
Portanto, x = 10 e y = 20
Determine CP na figura seguinte, sabendo que a // b // c.
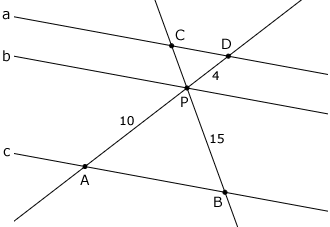
Solução
Pelo teorema de Tales, tem-se:
\(\dfrac{AP}{BP} = \dfrac{PD}{PC}\)
\(\dfrac{10}{15} = \dfrac{4}{PC}\)
PC = \(\dfrac{15 × 4}{10}\) = 6
Observação: Tenha cuidado ao construir a proporção. Note que os segmentos de uma mesma transversal focam todos nos numeradores ou todos nos denominadores das frações.
Considere duas retas retas paralelas cortadas por uma reta transversal, conforme ilustra a figura:
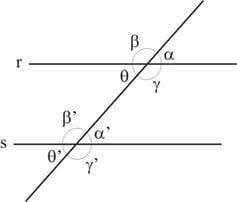
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.