Polígonos são regiões do plano cujos contornos são formados apenas por segmentos de reta.

Voltar Entendi

• Lados: são os segmentos que formam o contorno (\( \overline{AB} \), \( \overline{BC} \), \( \overline{CD} \), \( \overline{DE} \), \( \overline{EF} \) e \( \overline{FA} \)).
• Perímetro: é a medida da soma dos lados (\( \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{EF} + \overline{FA} \)).
• Vértices: pontos comuns a dois lados consecutivos (A, B, C, D, E e F).
• Ângulos: regiões formadas entre duas lados (\( \hat{A} \), \( \hat{B} \), \( \hat{C} \), \( \hat{D} \), \( \hat{E} \) e \( \hat{F} \)).
• Diagonais: são os segmentos que unem dois vértices não consecutivos (\( \overline{AC} \), \( \overline{AD} \), ..., \( \overline{FD} \)).

Voltar Entendi

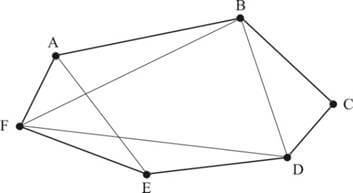
Temos dois tipos de polígonos: convexo e côncavo.

Um polígono é convexo quando dois quaisquer de seus pontos determinam um segmento totalmente contido no próprio polígono. Caso contrário, o polígono é côncavo.

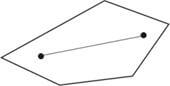polígono convexo

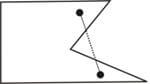polígono côncavo

Voltar Entendi

Os polígonos recebem nomes de acordo com o número de seus lados:

• 3 lados: triângulo
• 4 lados: quadrilátero
• 5 lados: pentágono
• 6 lados: hexágono
• 7 lados: heptágono
• 8 lados: octógono
• 9 lados: eneágono
• 10 lados: decágono
• 11 lados: undecágono
• 12 lados: dodecágono
• 15 lados: pentadecágono
• 20 lados: icoságono

Esses nomes são válidos, tanto para polígonos convexos como para côncavos.

Voltar Entendi

Em todo polígono convexo, temos que a soma dos ângulos internos é dada por:

S\(_i\) = (n - 2) ∙ 180º

onde n é o número de lados.

Assim, temos que a soma dos ângulos internos de qualquer:

• triângulo é 180º (teorema angular de Tales)
• quadrilátero é 360º
• pentágono é 540º
• e assim por diante

A soma dos ângulos externos de qualquer polígono convexo é 360º.

S\(_e\) = 360º

Voltar Entendi

Qual é o polígono , cuja soma dos ângulos internos vale 1.800º?

Solução

Segundo o enunciado, S\(_i\) = 1.800º.

Como S\(_i\) = (n - 2) ∙ 180º, tem-se:

1.800º = (n - 2) ∙ 180º ⇔ n - 2 = 10 ⇔ n = 12

O polígono de 12 lados chama-se duodecágono

Voltar Entendi

Três polígonos convexos tem n, n + 1, n + 2 lados respectivamente. Sendo 2.700º a soma de todos os ângulos internos dos três polígonos, determine o valor de n.

Solução

Sejam A, B e C os três polígonos de lados n, n + 1 e n + 2, respectivamente.

Então, a soma de cada um é dado por:

• Para o polígono de n lados: S\(_i\)A = (n - 2) ∙ 180º
• Para o polígono de n + 1 lados: S\(_i\)B = (n + 1 - 2) ∙ 180º ⇔ S\(_i\)B = (n - 1) ∙ 180º
• Para o polígono de n + 2 lados: S\(_i\)C = (n + 2 - 2) ∙ 180º ⇔ S\(_i\)C = n ∙ 180º

Segundo o enunciado, tem-se:

S\(_i\)A + S\(_i\)B + S\(_i\)C = 2.700º

Substituindo, vem:

(n - 2) ∙ 180º + (n - 1) ∙ 180º + n ∙ 180º = 2.700º

Colocando 180º em evidência:

180º ∙ (n - 2 + n - 1 + n) = 2.700º

3n - 3 = 2.700º/180º

3n - 3 = 15 ⇔ 3n = 15 + 3 ⇔ n = 18/3 = 6

Voltar Entendi

De cada vértice partem n - 3 diagonais. O número total de diagonais de polígono é determinado por:

D = \( \dfrac{n \cdot (n - 3)}{2} \)

onde n é o número de lados e n ≥ 3.

Voltar Entendi

Qual é o polígono cujo número de diagonais é o quádruplo do número de lados?

Solução

Sendo d o número de diagonais e n o número de lados, tem-se:

d = 4n

Como d = \( \dfrac{n \cdot (n - 3)}{2} \), basta substituir d:

4n = \( \dfrac{n \cdot (n - 3)}{2} \) ⇔ 8n = n\(^2\) - 3n

n\(^2\) - 11n = 0 ⇔ n(n - 11) = 0

• n = 0 (não serve pois não existe polígono cujo número de lados é igual a 0) ou
• n - 11 = 0 ⇔ n = 11

O polígono de 11 lados chama-se undecágono

Voltar Entendi

Qual o polígono que tem o número de lados iguais ao número de diagonais?

Solução

Sendo d o número de diagonais e n o número de lados, tem-se:

d = n

Como d = \( \dfrac{n \cdot (n - 3)}{2} \), basta substituir d:

n = \( \dfrac{n \cdot (n - 3)}{2} \) ⇔ 2n = n\(^2\) - 3n

n\(^2\) - 5n = 0 ⇔ n(n - 5) = 0

• n = 0 (não serve) ou
• n - 5 = 0 ⇔ n = 5

O polígono de 5 lados chama-se pentágono

Voltar Entendi

Um polígono é regular quando todos seus lados têm o mesmo tamanho e todos os seus ângulos internos são iguais.

Propriedades:

• Podemos calcular a medida \( a_i \) de cada um de seus ângulos internos: \( a_i = \dfrac{(n - 2) \cdot 180º}{n} \)
• Podemos calcular a medida \( a_e \) de cada um de seus ângulos externos: \( a_e = \dfrac{360º}{n} \)
• Todo polígono regular é inscritível numa circunferência, isto é, sempre é possível desenhar uma circunferência que passe por todos os vértices do polígono.
• Todo polígono regular é também circunscritível a uma circunferência, isto é, sempre é possível desenhar uma circunferência que tangencia todos os lados do polígono. Os pontos de tangência, são os pontos médios dos lados do polígono.

Voltar Entendi

• Centro: é o centro comum às circunferências inscrita e circunscrita.
• Apótema: é o segmento com extremidades no centro do polígono e no ponto médio de um lado do polígono (este segmento é perpendicular ao lado).
• Ângulo cêntrico: é o ângulo com vértice no centro do polígono e os lados contendo dois vértices consecutivos desse polígono.

Voltar Entendi

Perímetro é a soma do comprimento de todos os lados de um polígono.

Semiperímetro é a metade do perímetro.

Exemplo: Um terreno de 35 m de frente por 22 m de fundo (lateral), será cercado com um fio de arame. Quantos metros de fio são necessários para cercar todo o terreno?

P = 35 m + 22 m + 35 m + 22 m = 114 m

Logo, são necessários 114 m de fio para cercar o terreno.

Voltar Entendi

Dois polígonos são semelhantes quando possuem o mesmo número de lados e é possível estabelecer correspondência entre seus vértices tal que os ângulos correspondentes são congruentes e os lados correspondentes proporcionais.

Voltar Entendi

Num polígono regular, a\(_i\) - a\(_e\) = 60º. Qual é esse polígono?

Solução

Sabe-se que:

• \( a_i = \frac{(n - 2) \cdot 180º}{n} \)
• \( a_e = \dfrac{360º}{n} \)

Substituindo, vem:

\( \frac{(n - 2) \cdot 180º}{n} - \dfrac{360º}{n} \) = 60º

(n - 2) ∙ 180º - 360º = 60º ∙ n

Dividindo todos os termos por 60º, vem:

(n - 2) ∙ 3 - 6 = 1 ∙ n

3n - 6 - 6 = n ⇔ 2n = 12 ⇔ n = 6

O polígono que tem 6 lados chama-se hexágono

Voltar Entendi

O ângulo externo de um polígono regular é igual ao dobro do seu ângulo interno. Determine o número de diagonais desse polígono.

Solução

Sabe-se que:

• \( a_i = \frac{(n - 2) \cdot 180º}{n} \)
• \( a_e = \dfrac{360º}{n} \)
• \(a_e = 2 \cdot a_i\) (de acordo com o enunciado)

Substituindo, vem:

\( \dfrac{360º}{n} = 2 \cdot \frac{(n - 2) \cdot 180º}{n} \)

360º = 2 ∙ (n - 2) ∙ 180º

1 = n - 2 ⇔ n = 3

O polígono é um triângulo, que não possui diagonais.

Só para demonstrar, confira:

d = \( \dfrac{n \cdot (n - 3)}{2} \) = \( \dfrac{3 \cdot (3 - 3)}{2} \) = \( \dfrac{3 \cdot 0}{2} \) = 0

Portanto, o número de diagonais é zero

Voltar Entendi

Determine a medida de um ângulo cêntrico de um eneágono regular.

Solução

Um eneágono regular tem 9 lados. O ângulo cêntrico vale 360º/9 = 40º

Voltar Entendi