

Antes de explicar o que é função, veremos alguns conceitos importantes que nos ajudarão no estudo desta fascinante matéria.
O plano cartesiano é constituído por eixos coordenados (retas com escala) perpendiculares entre si (formam ângulo de 90º entre si) num ponto O (origem). Para o nosso estudo, adotaremos o plano cartesiano formado por 2 eixos:
Dados dois elementos a e b formamos um novo elemento indicado por (a; b) e denominado par ordenado, cujo primeiro elemento é o a e o segundo elemento é o b.
Impomos as seguintes condições de igualdade entre pares ordenados:
Exemplos:
Determinar x e y, de modo que os pares ordenados (2x + 1, 3) e (4x - y, y) sejam iguais.
Solução
Temos um sistemas com duas equações:
Substituindo (II) em (I), vem:
2x = 3 + 1 ⇔ 2x = 4 ⇔ x = 2
x = 2 e y = 3
Uma aplicação muito usada de pares ordenados é a que se verifica na representação de pontos no plano cartesiano, onde representa-se, genericamente, um ponto P do plano através de suas coordenadas x e y, escritas na forma (x; y), onde x é a abscissa e y é a ordenada do ponto P.
Exemplo: Sejam A = (1; 3) e B = (3; 1). Representando A e B no plano cartesiano, tem-se:
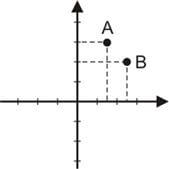
Observação: O primeiro elemento do par ordenado é sempre representado no eixo x e o segundo, no eixo y.
Dados dois conjuntos A e B, chama-se produto cartesiano de A por B o conjunto de todos os pares ordenados (x; y), onde x ∈ A e y ∈ B.
Notação: A×B = {(x; y) | x ∈ A e y ∈ B}
Exemplo:
Sejam A = {1, 5} e B = {w, m, p}, determine A×B, B×A, A×A e B×B:
a) por enumeração.
A×B = {(1; w), (1; m), (1; p), (5; w), (5; m), (5; p)}
B×A = {(w; 1), (w; 5), (m; 1), (m; 5), (p; 1), (p; 5)}
A×A = {(1; 1), (1; 5), (5; 1), (5; 5)}
B×B = {(w; w), (w; m), (w; p), (m; w), (m; m), (m; p), (p; w), (p; m), (p; p)}
b) por diagramas.
A×B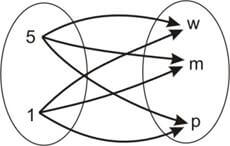 |
B×A |
A×A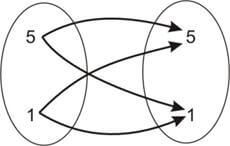 |
B×B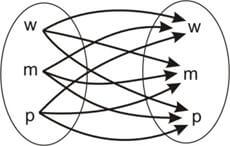 |
Observações:
Sejam dados 2 conjuntos não vazios A e B. Chama-se relação de A em B qualquer subconjunto de A×B.
Notação: R: A → B (relação de A em B)
Observação: Quando nos referirmos a relação de A em A, podemos também dizer apenas relação em A (R: A ⟶ A).
Seja R uma relação de A em B. Seja (x; y)∈ \(\mathbb{R}\). O elemento y é chamado imagem de x pela relação R.
Exemplo: Dada a relação
R = {(a; m), (b; n), (c; n), (d; p)}
Representando a relação graficamente, vem:
Neste exemplo, temos que o elemento m é imagem do elemento a, o elemento n é imagem dos elementos b e c e, por fim, o elemento p é imagem do elemento d.
Seja R uma relação de A em B.
Chama-se domínio da relação R o conjunto dos elementos de A que tem imagens em B.
Notação: D(R)
Chama-se conjunto imagem da relação R o conjunto dos elementos de B que são imagens de elementos de A.
Notação: Im(R)
Exemplo:
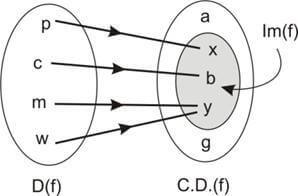
D(f) = {p, c, m, w} e Im(f) = {x, b, y}
Em álgebra, tem maior interesse as relações que são definidas por sentenças abertas nas variáveis x e y ou fórmulas que relacionam x e y no par (x; y). Essas fórmulas estabelecem uma lei de correspondência entre os elementos x e y de 2 conjuntos.
Exemplo:
Seja A = {1, 3, 5, 7} e seja a relação R em A (ou seja, de A em A), definida por R = {(x; y) ∈ A×A | x < y}.
Escrevendo a relação R, temos R = {(1; 3), (1; 5), (1; 7) , (3; 5), (3; 7) , (5; 7)}
Dada uma relação R de A em B, isto é, R contido em A B, chama-se inversa de R a relação R\(^{ }\) de B em A (isto é, R ⊂ B×A) tal que se (x; y) ∈ R, então (y; x) ∈ R\(^{ }\).
Exemplo: Considere a relação R = {(1; 3), (1; 5), (1; 7), (3; 5), (3; 7), (5; 7)}
Sua inversa é R^{-1} = {(3; 1), (5; 1), (7; 1), (5; 3), (7; 3), (7; 5)}
Seja R uma relação de A em B. Dizemos que R é uma função de A em B se e só se as seguintes condições se verificam:
Em outras palavras:
Sejam dois conjuntos A e B diferentes do vazio e seja f uma relação de A em B.
Diz-se que f é uma função (ou aplicação) de A em B se, e só se, todo elemento de A estiver associado, através de f, a um único elemento de B, tal que (x; y) ∈ f.
Observação: Pela definição de função, temos que função é um caso particular de relação, onde podemos dizer que toda função é uma relação. Mas cuidado, nem toda relação é uma função.
Notação: f: \(\mathbb{R} \rightarrow \mathbb{R} \)
Vamos ver alguns exemplos para entender melhor?
Considere os conjuntos A = {1, 2, 3, 4} e B = {a, b, c} e as relações f, g, h e i, de A em B, definidas por:
f = {(1; a), (3; c), (4; b)}
A relação f não é função de A em B, pois o elemento 2 ∈ A não associa nenhum elemento de B.
Considere os conjuntos A = {1, 2, 3, 4} e B = {a, b, c} e as relações f, g, h e i, de A em B, definidas por:
g = {(1; a), (2; b) , (3; c) , (4; a) , (4; c)}
A relação g não é função de A em B, pois e elemento 4 ∈ A associa-se com dois elementos distintos de B (a e c).
Considere os conjuntos A = {1, 2, 3, 4} e B = {a, b, c} e as relações f, g, h e i, de A em B, definidas por:
h = {(1; a), (2; a), (3; a), (4; a)}
A relação h é função, pois cada elemento de A está associado com apenas um elemento de B. Observe que todos os elementos de A estão associados ao elemento a de B.
Considere os conjuntos A = {1, 2, 3, 4} e B = {a, b, c} e as relações f, g, h e i, de A em B, definidas por:
i = {(1; a), (2; b), (3; a), (4; c)}
A relação i é função, pois cada elemento de A está associado com apenas um elemento de B.
São funções definidas por sentenças abertas nas variáveis x e y ou fórmulas que relacionam x e y no par (x; y). Essas fórmulas estabelecem uma lei de correspondência entre os elementos x e y de 2 conjuntos.
Seja a função f: A → B.
O conjunto A é chamado domínio da função f (ou conjunto de partida) e o conjunto B é o contradomínio de f (ou conjunto de chegada).
Os elementos de B que são imagens dos elementos de A pela função f constituem o conjunto imagem de f e são denotados por y = f(x).
A partir de agora iremos aprender o que são e as diferenças entre as funções injetoras, sobrejetoras e bijetoras.
Seja a função f: A → B. f é injetora (ou injetiva, ou injeção) se e só se elementos distintos de A tem imagens distintas em B, isto é, ∀x\(_1\), x\(_2\) ∈ A, x\(_1\) ≠ x\(_2\) ⇒ f(x1) ≠ f(x2).
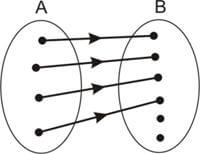
Seja a função f : A → B. f é sobrejetora (ou sobrejetiva, ou sobrejeção) se e só se ∀ ∈ B, existe x ∈ A tal que y = f(x), isto é, todos os elementos do contradomínio B são imagens.
Então f : A → B é sobrejetora se e só se a Im(f) = B.
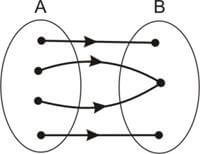
Seja a função f : A → B. f é bijetora (ou bijetiva, ou bijeção) se e só se f é injetora e sobrejetora.
Você sabia que uma função pode ser par, ímpar ou não ter paridade?
Pois é! A partir de agora iremos explorar a paridade de funções.
Sejam A, B ⊂ \( \mathbb{R} \). Seja f: A → B. f é função par se e só se ∀x ∈ A, tem se f(x) = f(-x), isto é, f é função par se elementos opostos tem a mesma imagem.
Sejam A, B ⊂ \( \mathbb{R} \). Seja f: A → B. f é função ímpar se e só se ∀x ∈ A, tem se f(x) = -f(-x), isto é, f é função ímpar se elementos opostos tem imagens opostas.
É toda função que não é nem par e nem ímpar.
Agora iremos aprender os tipos de crescimento das funções. Dependendo do sentido da função, ela pode ser:
Funções monótonas são funções que não mudam o sentido de crescimento.
Sejam A, B ⊂ \( \mathbb{R} \). Uma função f: A → B é crescente se e só se ∀x\(_1\), x\(_2\) ∈ A, vale:
x\(_1\) < x\(_2\) ⇒ f(x\(_1\)) < f(x\(_2\))
Sejam A, B ⊂ \( \mathbb{R} \). Uma função f: A → B é crescente se e só se ∀x\(_1\), x\(_2\) ∈ A, vale:
x\(_1\) < x\(_2\) ⇒ f(x\(_1\)) ≤ f(x\(_2\))
Sejam A, B ⊂ \( \mathbb{R} \). Uma função f: A → B é decrescente se e só se ∀x\(_1\), x\(_2\) ∈ A, vale:
x\(_1\) < x\(_2\) ⇒ f(x\(_1\)) > f(x\(_2\))
Sejam A, B ⊂ \( \mathbb{R} \). Uma função f: A → B é decrescente se e só se ∀x\(_1\), x\(_2\) ∈ A, vale:
x\(_1\) < x\(_2\) ⇒ f(x\(_1\)) ≥ f(x\(_2\))
Sejam A, B ⊂ \( \mathbb{R} \). Uma função f: A → B é constante se, e só se, f(x) = k, ∀x ∈ A. Isto é Im(f) = {k}.
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.