

Função do 2º grau (ou função quadrática) é toda função do tipo
f(x) = ax² + bx + c
com a, b, c ∈ \( \mathbb{R} \) e a ≠ 0.
Exemplos:
Agora é com vc! Complete a tabela da função f(x) = x² – 4x – 3.
| x | f(x) |
| -3 | 18 |
| -2 | |
| -1 | |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 |
O gráfico de uma função quadrática é uma curva denominada parábola.
Dependendo do sinal de a, temos dois casos:
Caso 1: a < 0 → a concavidade da parábola é voltada para baixo.
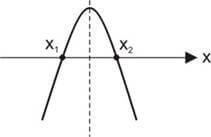
Caso 2: a > 0 → a concavidade da parábola é voltada para cima.
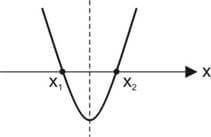
O gráfico corta o eixo y em c.
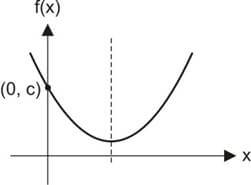
Para o discriminante ∆, temos:
∆ < 0 → A parábola não corta o eixo x (não têm raízes reais)
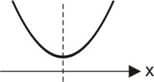
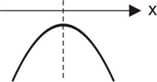
∆ = 0 → A parábola tangencia o eixo x (duas raízes reais e iguais)
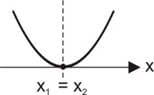
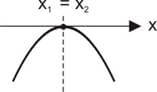
∆ > 0 → A parábola corta o eixo x em dois pontos distintos (duas raízes reais e distintas)


Vértice da parábola: \( V(x_V, y_V) \Leftrightarrow V\left( -\dfrac{b}{2a}, -\dfrac{\Delta}{4a} \right) \).
Máximo e mínimo (\(y_V\)):
Se a < 0, a função apresentará ponto de máximo.

Se a > 0, a função apresentará ponto de mínimo.

Considere a equação do 2º grau, f(x) = a x² + bx + c, sabendo-se que f(0) = 5, f(1) = 3 e f(-1) = 1, calcule:
Solução
a) De acordo com os dados, tem-se:
f(0) = 5
a (0)² + b(0) + c = 5
c = 5
f(1) = 3
a(1)² + b(1) + 5 = 3
a + b + 5 = 3
a + b = - 2 (I)
f(-1) = 1
a(-1)² + b(-1) + 5 = 1
a – b = - 4 (II)
Somando (I) e (II), vem:
(I) + (II) = a + b + a – b = - 2 - 4
2a = - 6
a = -3
Substituindo a = -3, em (I), vem:
a + b = - 2
(-3) + b = -2
b = -2 + 3 = 1
Portanto, a = -3, b = 1 e c = 5
b) Após encontrarmos os coeficientes a, b e c, sabemos que
f(x) = -3x² + x + 5
Então, para determinar f(10) basta substituir x por 10
f(10) = -3(10)² + (10) + 5 = -3(100) + 15 = -285
Esboce o gráfico da função y = 2x²
Solução
Este exercício será resolvido por meio de uma tabela:
| x | y |
|---|---|
| -2 | 8 |
| -1 | 2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 8 |
De acordo com a tabela, constrói-se o gráfico:

Denomina-se zero ou raiz da função f(x) = ax² + bx + c, com a ≠ 0, o valor de x que anula a função, isto é, torna f(x) = 0.
Fazendo f(x) = ax² + bx + c = 0 tem-se que as raízes de f(x) são as raízes da equação do 2º grau ax² + bx + c = 0.
Esboce o gráfico da função y = -4x² + 36
Solução
Este exercício será resolvido sem o uso da tabela. Para isso, deve-se obter as raízes e o vértice da parábola
Note que:
Raízes:
-4x² + 36 = 0 ⇔ 4x² = 36 ⇔ x² = 9 ⇔ x = ±3
Como a < 0, a parábola tem concavidade voltada para baixo.
Vértice:
\(x_V = -\dfrac{b}{2a} = -\dfrac{0}{2(-4)}\) = 0
∆ = b² - 4ac = (0)² - 4(-4)(36) = 576
\(y_V = -\dfrac{\Delta}{4a} = -\dfrac{576}{4(-4)}\) = 36
Com as raízes e o vértice obtidos, pode-se construir o gráfico:
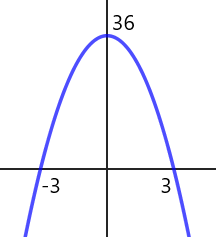
Observação: O gráfico de y = ax² + bx + c corta o eixo das ordenadas em (0, c).
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.