Logotipo da Matintera
Home Ensino Fundamental II 8º ano Matemática Álgebra Conjunto dos números reais

O conjunto dos números reais \(\mathbb{R}\) é a união do conjunto dos racionais \(\mathbb{Q}\) com o conjunto dos irracionais \(\mathbb{I}\)

\(\mathbb{R}\) = \(\mathbb{Q} \cup \mathbb{I}\).

Como o conjuntos dos racionais contém o conjunto dos inteiros, que por sua vez contém o conjunto dos naturais, temos o seguinte diagrama:

Diagrama de Venn dos conjuntos numéricos

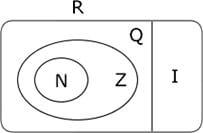
Repare no diagrama que:

  • \(\mathbb{N}\) ⊂ \(\mathbb{Z}\) ⊂ \(\mathbb{Q}\) ⊂ \(\mathbb{R}\)
  • \(\mathbb{I}\) ⊂ \(\mathbb{R}\)
  • \(\mathbb{Q}\) ∩ \(\mathbb{I}\) = ∅

Observação:

  • O sinal * (asterisco) elimina o número zero de um conjunto.
  • O sinal + (mais) elimina os números negativos de um conjunto.
  • O sinal – (menos) elimina os números positivos de um conjunto.

Exemplos:

  • \( \mathbb{Z}^* \) = {..., -2, -1, 1, 2, 3, ...}
  • \( \mathbb{Z}_+ \) = {0, 1, 2, 3, ...}
  • \( \mathbb{Z}_- \) = {..., -2, -1, 0}
  • \( \mathbb{Z}^*_+ \) = {1, 2, 3, 4, ...}

O conjunto dos números reais positivos é representado por

Os intervalos lineares são subconjuntos do conjunto dos números reais e podem ser:

  • Finitos: quando estão compreendidos entre dois extremos definidos
  • Infinitos: quando possuem apenas um extremo definido ou nenhum extremo

Alguns subconjuntos de \(\mathbb{R}\) tem notações especiais:

H = {x ∈ \(\mathbb{R}\) | a ≤ x ≤ b} é formado por todos os números reais compreendidos entre a e b, inclusive a e b. Este subconjunto de \(\mathbb{R}\), recebe o nome de intervalo fechado de extremos a e b.

Intervalos lineares finitos fechado em a e b

J = {x ∈ \(\mathbb{R}\) | d < x < h} é formado por todos os números reais compreendidos entre d e h, exclusive d e h. Este subconjunto de \(\mathbb{R}\), recebe o nome de intervalo aberto de extremos d e h.

Intervalos lineares finitos aberto em d e h

K = {x ∈ \(\mathbb{R}\) | c ≤ x < j} é formado por todos os números reais compreendidos entre c e j, inclusive c e exclusive j. Este subconjunto de \(\mathbb{R}\), recebe o nome de intervalo fechado à esquerda e aberto à direita de extremos c e j.

Intervalos lineares finitos fechado em c e aberto em j

L = {x ∈ \(\mathbb{R}\) | m < x ≤ n} é formado por todos os números reais compreendidos entre m e n, exclusive m e inclusive n. Este subconjunto de \(\mathbb{R}\), recebe o nome de intervalo aberto à esquerda e fechado à direita de extremos m e n.

Intervalos lineares finitos aberto em m e fechado em n

Sendo a um número real qualquer, os intervalos infinitos são conjuntos da forma:

{x ∈ \(\mathbb{R}\) | x ≤ a} = ]–∞; a] = (–∞; a]

Intervalos lineares infinitos menor ou igual a a

{x ∈ \(\mathbb{R}\) | x < a} = ]–∞; a[ = (–∞; a)

Intervalos lineares infinitos menor que a

{x ∈ \(\mathbb{R}\) | x ≥ a} = [a; ∞[ = [a; ∞)

Intervalos lineares infinitos maior ou igual a a

{x ∈ \(\mathbb{R}\) | x > a} = ]a; ∞[ = (a; ∞)

Intervalos lineares infinitos maior que a

Observação: \(\mathbb{R}\) = ]–∞; ∞[ = (–∞;∞)

Intervalos lineares infinitos

Classifique em V (verdadeiro) ou F (falso)

  • a) Se a ∈ \(\mathbb{I}\) e B ∈ \(\mathbb{I}\), então (a + b) ∈ \(\mathbb{I}\)
  • b) Se a ∈ \(\mathbb{I}\) e B ∈ \(\mathbb{I}\), então (a ∙ b) ∈ \(\mathbb{I}\)

Solução

a) Para provar que uma afirmação é falsa, basta apresentar um exemplo que comprove a falsidade.

\(\sqrt{3}\) ∈ \(\mathbb{I}\) e -\(\sqrt{3}\) ∈ \(\mathbb{I}\). Mas a soma \(\sqrt{3}\) + (-\(\sqrt{3}\)) = 0. 0 ∉ \(\mathbb{I}\). F

b) Considere os mesmos dados do item anterior.

\(\sqrt{3}\) ∙ (-\(\sqrt{3}\)) = \(\sqrt{3}^2\) = 3. 3 ∉ \(\mathbb{I}\). F

Determine uma propriedade para os conjuntos D(12) e M(2), onde D é o conjunto dos divisores e M o conjunto dos múltiplos

Solução

D(12) = {x ∈ Z | x divide 12}

M(2) = {x ∈ Z | x é múltiplo de 2}

Esta foi uma demonstração gratuita.

Logue para ter acesso a todo conteúdo interativo.

Hum, ainda não criou conta!?

Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.

Criar conta Login