Triângulos são polígonos de três lados.

PROPRIEDADES ANGULARES

Soma dos ângulos internos: A soma dos três ângulos internos de um triângulo é sempre igual a 180º.

Soma dos ângulos externos: A soma dos três ângulos externos de um triângulo é sempre igual a 360º.

TEOREMA DO ÂNGULO EXTERNO

Cada ângulo externo é igual à soma dos dois ângulos internos não adjacentes.

Entendi

Num triângulo ABC, as medidas dos ângulos internos de vértices A, B e C são dadas por 3x, 2x - 10º e 3x + 30º, respectivamente. Determine cada ângulo interno desse triângulo.

Solução

A soma dos ângulos internos de um triângulo vale 180º. Então:

3x + 2x - 10º + 3x + 30º = 180º

8x + 20º = 180º

8x = 180º - 20º

x = 160º/8 = 20º

Ângulo interno de vértice A: 3x = 3(20º) = 60º

Ângulo interno de vértice B: 2x - 10º = 2(20º) - 10º = 40º - 10º = 30º

Ângulo interno de vértice C: 3x + 30º = 3(20º) + 30º = 60º + 30º = 90º

Voltar Entendi

Num triângulo ABC, as medidas dos ângulos internos de vértices B e C são dadas por 2x + 10º e 4x - 40º, respectivamente. Se a medida do ângulo externo de vértice A é 5x, determine cada ângulo interno desse triângulo.

Solução

De acordo com o enunciado, tem-se a seguinte figura:

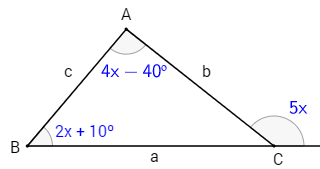
Pelo teorema do ângulo externo, tem-se:

5x = 2x + 10º + 4x - 40º

5x - 2x - 4x = 10º - 40º

- x = - 30º

x = 30º

Ângulo interno de vértice A:

5x + y = 180º

5(30º) + y = 180º

y = 180º - 150º = 30º

Ângulo interno de vértice B:

2x + 10º = 2(30º) + 10º = 60º + 10º = 70º

Ângulo interno de vértice C:

4x - 40º = 4(30º) - 40º = 120º - 40º = 80º

Voltar Entendi

Os triângulos podem ser classificados de acordo com seus lados e ângulos.

Quanto aos lados

• Escaleno: 3 lados de medidas diferentes. Os 3 ângulos internos também possuem medidas diferentes.
• Isósceles: 2 lados de medidas iguais. 2 de seus ângulos internos possuem mesma medida.
• Equilátero: 3 lados de medidas iguais. Os 3 ângulos internos possuem mesma medida.

Quanto aos ângulos

• Acutângulo: todos os seus ângulos internos são agudos.
• Retângulo: 1 ângulo interno é reto.
• Obtusângulo: 1 ângulo interno é obtuso.

Num triângulo que tem dois lados de medidas iguais (isósceles), o terceiro lado é chamado base e o ângulo oposto à base é chamado ângulo vértice.

Num triângulo retângulo os lados adjacentes ao ângulo reto são chamados catetos e o lado oposto ao ângulo reto é a hipotenusa.

Voltar Entendi

Num triângulo ABC, as medidas dos ângulos internos de vértices A, B e C são dadas por 3x, 2x - 10º e 3x + 30º, respectivamente. Classifique-o quanto aos lados e ângulos.

Solução

Este exercício foi resolvido anteriormente e o triângulo em questão possui como ângulos internos 60º, 30º e 90º.

Note que o triângulo é retângulo pois possui um ângulo de 90º.

Note, ainda, que os três ângulos são diferentes. Logo, seus lados são diferentes e, assim, pode-se afirmar que o triângulo é escaleno.

O triângulo ABC é retângulo e escaleno

Voltar Entendi

Num triângulo ABC, as medidas dos ângulos internos de vértices B e C são dadas por 2x + 10º e 4x - 40º, respectivamente. Se a medida do ângulo externo de vértice A é 5x, determine cada ângulo interno desse triângulo.

Solução

Este exercício foi resolvido anteriormente e o triângulo em questão possui como ângulos internos 30º, 70º e 80º.

Note que o triângulo é acutângulo pois seus ângulos são menores do que 90º.

Note, ainda, que os três ângulos são diferentes. Logo, seus lados são diferentes e, assim, pode-se afirmar que o triângulo é escaleno.

O triângulo ABC é acutângulo e escaleno

Voltar Entendi

Sejam a, b e c as medidas de três segmentos. Estes segmentos são lados de um triângulo se e só se, qualquer que seja o segmento, sua medida esteja compreendida entre o módulo da diferença e a soma dos outros dois segmentos.

• |a - b| < c < a + b
• |a - c| < b < a + c
• |b - c| < a < b + c

Voltar Entendi

Verifique se os lados 3, 4 e 5 formam um triângulo.

Solução

• |3 - 4| < 5 < 3 + 4 ↔ |-1| < 5 < 7 ↔ 1 < 5 < 7 (V)
• |3 - 5| < 4 < 3 + 5 ↔ |-2| < 4 < 8 ↔ 2 < 4 < 8 (V)
• |4 - 5| < 3 < 4 + 5 ↔ |-1| < 3 < 9 ↔ 1 < 3 < 9 (V)

Como satisfaz as condições, os lados 3, 4 e 5 formam um triângulo

Voltar Entendi

Verifique se os lados 3, 6 e 10 formam um triângulo.

Solução

• |3 - 6| < 10 < 3 + 6 ↔ |-3| < 10 < 9 ↔ 3 < 10 < 9 (F)
• |3 - 10| < 6 < 3 + 10 ↔ |-7| < 6 < 13 ↔ 7 < 6 < 13 (F)
• |6 - 10| < 3 < 6 + 10 ↔ |-4| < 3 < 16 ↔ 4 < 3 < 16 (F)

Para que não forme triângulo, basta que pelo menos uma condição não seja satisfeita.

Neste caso, nenhuma condição foi satisfeita. Logo, os lados 3, 6 e 10 não formam um triângulo

Voltar Entendi

Sendo a o maior lado de um triângulo, temos que, se:

• a² < b² + c² → triângulo acutângulo
• a² = b² + c² → triângulo retângulo
• a² > b² + c² → triângulo obtusângulo

Voltar Entendi

Verifique a natureza de um triângulo cujos lados medem 3, 4 e 5.

Solução

O maior lado é 5. Substituindo em:

a² b² + c² (o ponto de interrogação será determinado no final, podendo ser <, > ou =)

vem:

5² 4² + 3²

25 16 + 9

25 25

25 = 25

Logo, o triângulo é retângulo

Voltar Entendi

Verifique a natureza de um triângulo cujos lados medem 3, 7 e 8.

Solução

O maior lado é 8. Substituindo em:

a² b² + c² (o ponto de interrogação será determinado no final, podendo ser <, > ou =)

vem:

8² 7² + 3²

64 49 + 9

64 58

64 > 58

Logo, o triângulo é obtusângulo

Voltar Entendi

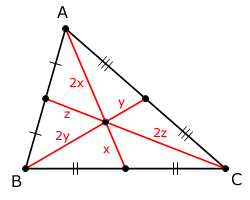
Mediana: Mediana é o segmento que une um vértice ao ponto médio do lado oposto.

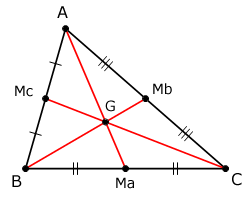
As três medianas de qualquer triângulo passam por um mesmo ponto (G), chamado baricentro do triângulo.

Altura: Altura é o segmento que une um vértice ao lado oposto (ou ao prolongamento deste), sendo perpendicular ao mesmo.

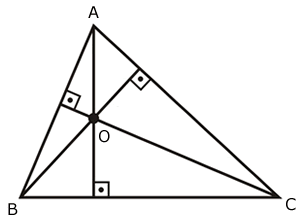
As três alturas de qualquer triângulo passam por um mesmo ponto (O), chamado ortocentro do triângulo.

Bissetriz interna: Bissetriz interna é o segmento contido no triângulo, que divide o ângulo interno em dois ângulos iguais.

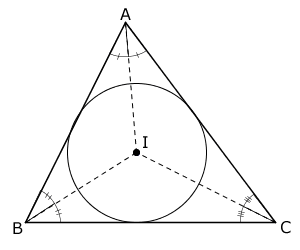
As três bissetrizes internas de qualquer triângulo passam por um mesmo ponto (I), chamado incentro (centro da circunferência inscrita no triângulo) do triângulo.

Mediatriz: Mediatriz é a reta perpendicular ao lado, passando pelo ponto médio do mesmo.

As três mediatrizes de qualquer triângulo passam por um mesmo ponto (E), chamado circuncentro (centro da circunferência circunscrita ao triângulo) do triângulo.

Voltar Entendi

TRIÂNGULO QUALQUER

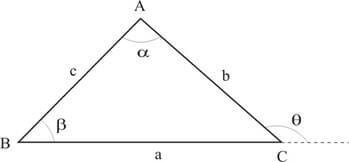
Para todo triângulo, independente do seu tipo, temos as seguintes propriedades:

• O baricentro de um triângulo divide cada mediana na razão 2 para 1, a partir de cada vértice.
  
• Cada ângulo externo é igual à soma dos dois ângulos internos não adjacentes (Teorema do ângulo externo).

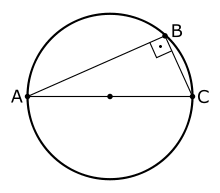
TRIÂNGULO RETÂNGULO

Para todo triângulo retângulo temos as seguintes propriedades:

• Todo triângulo retângulo pode ser inscrito numa semicircunerência, cujo diâmetro é igual à hipotenusa do triângulo.
  
• A mediana relativa à hipotenusa tem por medida a metade da medida da hipotenusa. Essa mediana divide o triângulo em dois triângulos isósceles.
  
• Todo triângulo retângulo que possui um ângulo de 30º, o cateto oposto a esse ângulo tem como medida a metade da hipotenusa.
• A altura relativa à hipotenusa de um triângulo retângulo divide o ângulo reto em dois ângulos cujas medidas são iguais aos ângulos agudos do triângulo.

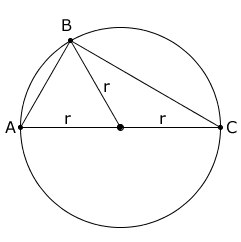
TRIÂNGULO ISÓSCELES

Para todo triângulo isósceles temos as seguintes propriedades:

• Num triângulo isósceles, os dois ângulos adjacentes à base são iguais.
• A mediana traçada em relação à base é também altura, mediatriz e bissetriz interna.

TRIÂNGULO EQUILÁTERO

Para todo triângulo equilátero temos as seguintes propriedades:

• Num triângulo equilátero, os três ângulos são iguais.
• A mediana traçada em relação a qualquer um dos lados é também altura, mediatriz e bissetriz interna.
• O baricentro G é também ortocentro, incentro e circuncentro.
• O raio R da circunferência circunscrita é o dobro do raio da circunferência inscrita.

Voltar Entendi

Dois triângulos são semelhantes se, e só se, é possível estabelecer uma correspondência entre seus vértices de modo que:

• a) os ângulos correspondentes são congruentes; e
• b) os lados correspondentes são proporcionais.

CASOS DE SEMELHANÇA

Dois triângulos são semelhantes se:

• ângulo-ângulo (AA): eles têm dois ângulos congruentes.
• lado-ângulo-lado (LAL): eles têm dois lados proporcionais e os ângulos compreendidos entre eles congruentes.
• lado-lado-lado (LLL): eles têm os três lados proporcionais.

Propriedades:

• Se dois triângulos são semelhantes, seus elementos correspondentes como altura, mediana, bissetriz etc, são proporcionais, ou seja, quaisquer dois segmentos correspondentes são proporcionais a dois lados correspondentes.
• Se dois triângulos são semelhantes, com razão de semelhança igual a k, então a razão entre as alturas correspondentes, os lados correspondentes, as bissetrizes correspondentes, as medianas correspondentes, os perímetros, também é k. A razão entre as áreas, é igual a k².
• Em todo triângulo, um segmento paralelo a um dos lados e que intercepta os outros dois determina um novo triângulo semelhante ao primeiro.
• Em todo triângulo, o segmento que une os pontos médios de dois lados é paralelo ao terceiro lado e igual à sua metade (base média).

Voltar Entendi

Em todo triângulo, a bissetriz de um ângulo interno divide o lado oposto a esse ângulo em segmentos proporcionais aos lados adjacentes ao ângulo.

No triângulo ABC ao lado, a bissetriz do ângulo  é o segmento \( \overline{AD} \).

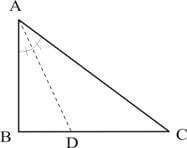
Temos que:

\( \dfrac{BD}{AB} = \dfrac{DC}{AC} \)

Voltar Entendi

Em todo triângulo, a bissetriz de um ângulo externo, intercepta a reta suporte do lado oposto, dividindo externamente este lado em segmentos proporcionais aos lados adjacentes ao ângulo.

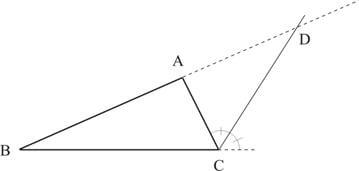
No triângulo ABC ao lado, a bissetriz do ângulo é o segmento \( \overline{CD} \).

Temos que:

\( \dfrac{BD}{BC} = \dfrac{AD}{AC} \)

Voltar Entendi

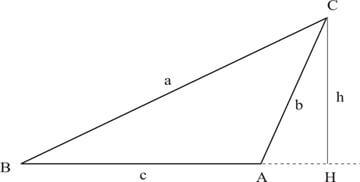
TRIÂNGULO ACUTÂNGULO

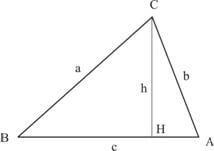
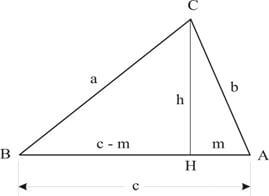
a² = b² + c² - 2 ∙ c ∙ m

TRIÂNGULO OBTUSÂNGULO

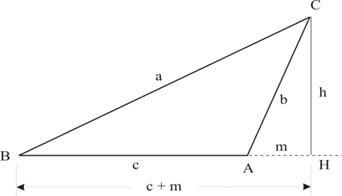
a² = b² + c² + 2 ∙ c ∙ m

Voltar Entendi

Considere o triângulo retângulo na figura:

• b² = a ∙ n
• c² = a ∙ m
• h² = m ∙ n
• b ∙ c = a ∙ h

Voltar Entendi

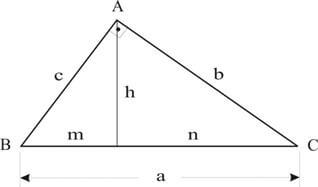
Considere o triângulo retângulo na figura:

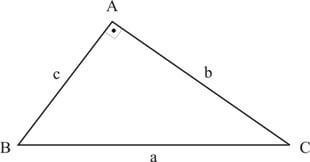
a² = b² + c²

Voltar Entendi