

Nessa seção iremos observar e aprender algumas noções primitivas de geometria plana:
Observe as figuras:
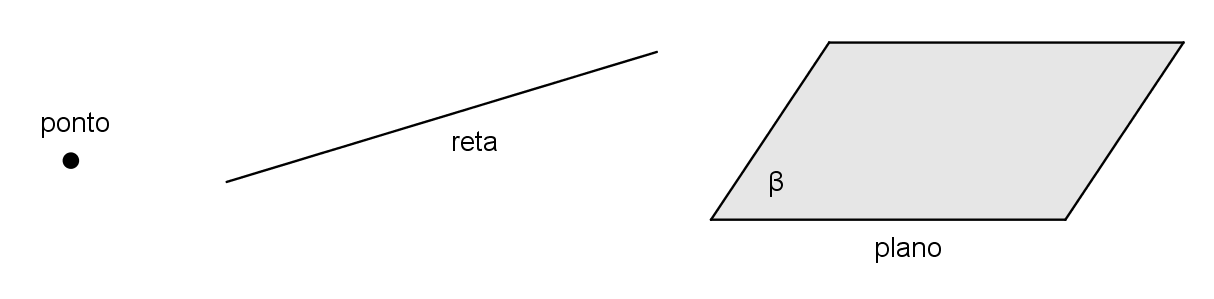
O ponto é o menor elemento da Geometria. A partir dele podemos criar outras figuras, como a reta e o plano.
Você sabe qual figura iremos criar se colocarmos diversos pontos alinhados em sequência?
•••••••••••••••••••••••••••••••••
Isso mesmo, formamos uma reta! Se colocarmos mais pontos alinhados nos espaços entre um ponto e outro teremos a seguinte figura:
_______________________
Observação: Ter pontos alinhados significa dizer que eles são colineares (mesma linha).
Você sabe qual figura iremos criar se colocarmos diversas retas uma ao lado da outra e na mesma direção em sequência?
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Isso mesmo, formamos um plano! Se colocarmos mais retas alinhadas nos espaços entre uma reta e outra teremos a seguinte figura:
██████████████
Observação: Ter retas uma ao lado da outra e na mesma direção significa dizer que elas são paralelas distintas. Se as retas estiverem na mesma direção mas uma sobre a outra dizemos que elas são paralelas coincidentes.
Se um plano é formado por diversas retas e uma reta é formada por diversos pontos, podemos afirmar, com toda certeza do mundo, que uma plano pode ser formado por diversos pontos?
•••••••••••••••••••••••••••••••
•••••••••••••••••••••••••••••••
•••••••••••••••••••••••••••••••
•••••••••••••••••••••••••••••••
Então, concluímos que
Depois do que você viu, observe que
(1) Para traçar uma reta basta ter 2 pontos
(2) Duas retas paralelas distintas determinam um único plano
A soma das verdadeiras é
Por 2 retas paralelas distintas passa(m)
Por 2 retas paralelas coincidentes passa(m)
Observe as figuras:

Na primeira figura temos um pedaço de reta limitada por 2 pontos em suas extremidades. Esta figura é um segmento de reta. Note que ela é representada por uma barra sobre a união dos nomes dos pontos: \(\overline{AB}\).
Na segunda figura temos uma reta com 1 ponto em uma de suas extremidades. Esta figura é uma semi-reta (como se fosse meia reta). A outra extremidade não tem fim (representado pela seta). Note que ela é representada por uma seta sobre o nome do ponto: \(\overrightarrow{X}\).
E na terceira figura temos uma reta passando por 2 pontos, mas esses pontos não a delimitam. Esta figura é uma reta. Note que ambas as extremidades não tem fim. Note que ela é representada por uma seta bidirecional sobre a união dos nomes dos pontos: \(\overleftrightarrow{EF}\).
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.