

No popular, ângulo é a região compreendida entre dois lados que possuem um ponto em comum, chamado de vértice.
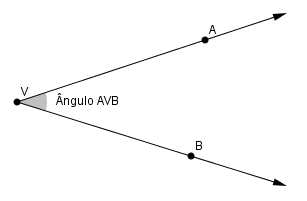
Um ângulo α pode ser:
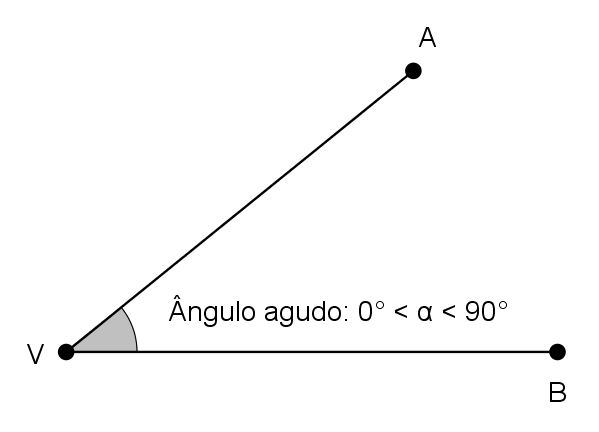
Ângulo agudo
O ângulo é agudo quando está compreendido entre 0º e 90º (0º < α < 90º)
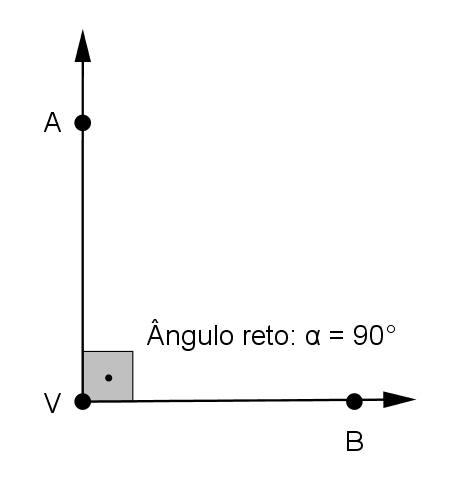
Ângulo reto
O ângulo é reto quando é igual a 90º (α = 90º)
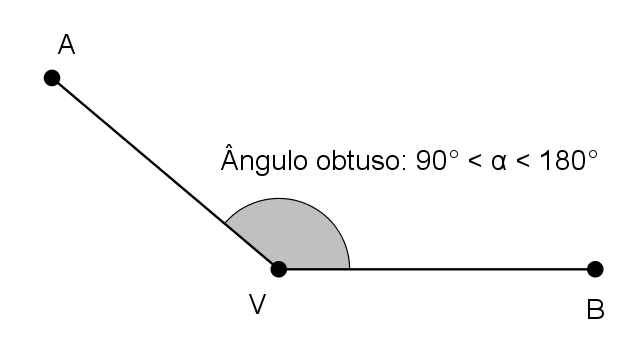
Ângulo obtuso
O ângulo é obtuso quando está compreendido entre 90º e 180º (90º < α < 180º)
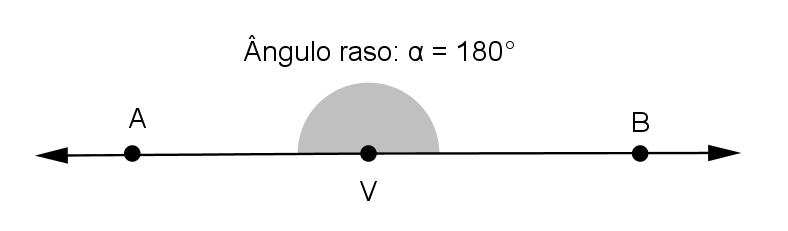
Ângulo raso
O ângulo é raso quando é igual a 180º (α = 180º)

Quais ângulos são agudos?
O ângulo 135º é um ângulo

O ângulo da figura é um ângulo
Dois ângulos α e β podem ser:
Ângulos complementares
Dois ângulos são complementares quando a soma entre eles é 90º:
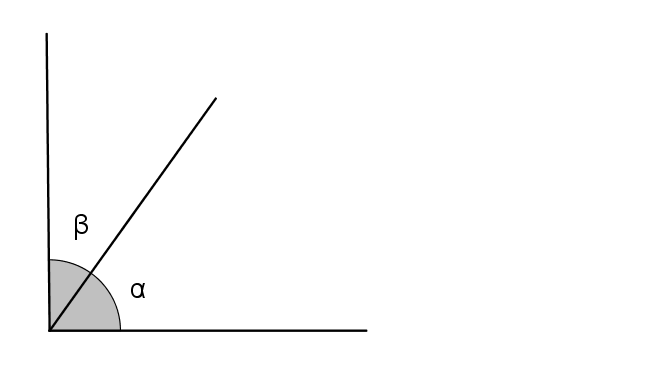
α + β = 90º
Ângulos suplementares
Dois ângulos são suplementares quando a soma entre eles é 180º:

α + β = 180º
Ângulos opostos pelo vértice (OPV)
São ângulos formados pelas mesmas retas e que se encontram opostos pelo ponto em comum (vértice) das retas.
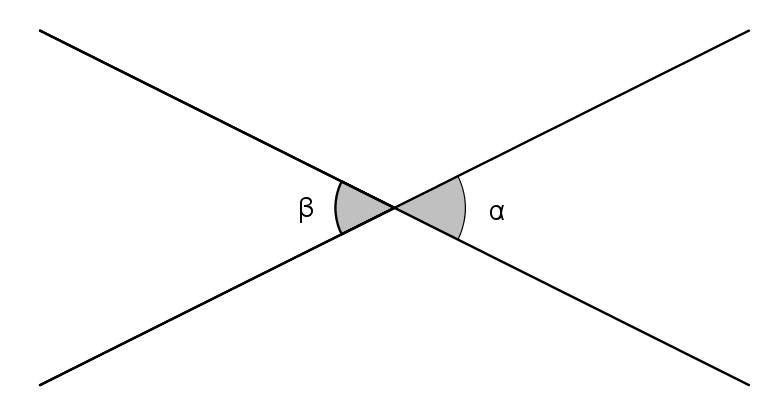
α = β
Observe que ângulos opostos pelo vértice são sempre congruentes, ou seja, possuem medidas iguais.
Bissetriz de um ângulo é a semi-reta de origem no vértice do ângulo e que o divide em dois ângulos iguais.
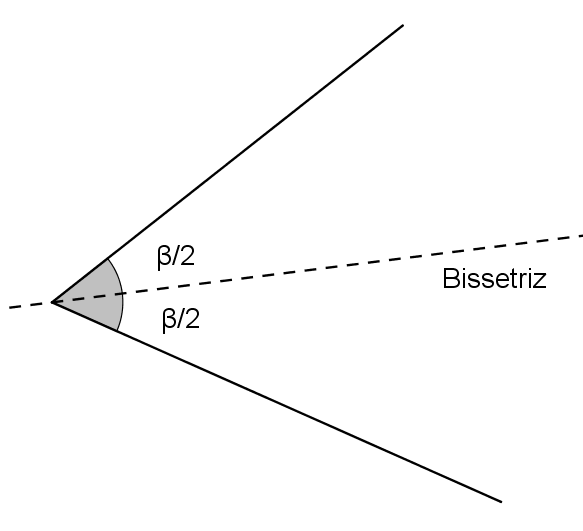
A principal unidade utilizada para medir ângulos é o grau (º).
1 grau equivale a 60 minutos. Como 1 minuto equivale a 60 segundos, 1 grau equivale a 3.600 segundos.
Assim:
1º ⇔ 60' ⇔ 3.600"
Os ângulos podem ser somados, multiplicados, subtraídos e divididos. Para fazer isso, no entanto, é necessário considerar suas sub-unidades (minutos e segundos). Há casos em que é necessário fazer transformações com medidas de ângulos durante essas operações.
43º 18' 20'' + 25º 18' 30''
43º 18' 20'' + 25º 18' 30'' = 68º 36' 50''
10º 36' 30'' + 23º 45' 50''
10º 36' 30'' + 23º 45' 50'' = 33º 81' 80''
Note que 80'' é igual a 1' 20''. Este 1' somamos aos minutos. Assim, tem-se que 33º 81' 80'' = 33º 82' 20''
Note, agora, que 82' é igual a 1º 22''. Este 1º somamos aos graus. Assim, tem-se que 33º 82' 20'' = 34º 22' 20''
90º – 35º 49' 46''
Vamos apresentar 90º com as casas dos minutos e dos segundos.
90º = 89º 60' ("empresta-se" 1º para os minutos)
89º 60' = 89º 59' 60'' ("empresta-se" 1' para os segundos)
Assim, tem-se que 90º = 89º 59' 60''
Fazendo 89º 59' 60'' - 35º 49' 46'':
89º 59' 60'' - 35º 49' 46'' = 54º 10' 14''
Dois ângulos consecutivos e de mesmo vértice são chamados de ângulos adjacentes.
Na figura, o ângulo raso XÂY é dividido em três ângulos pelas semi-retas \(\overrightarrow{AM}\) e \(\overrightarrow{AN}\) de modo que MÂN = 2 ∙ XÂM e NÂY = XÂM + 20º. Determine os ângulos XÂM, MÂN e NÂY.
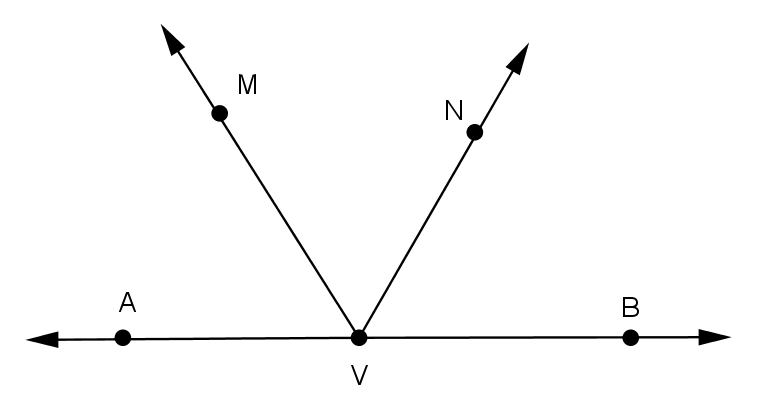
O ângulo XÂY é raso, logo XÂY = 180º.
Note que XÂM + MÂN + NÂY = XÂY
Chamando XÂM = x, tem-se, de acordo com o enunciado:
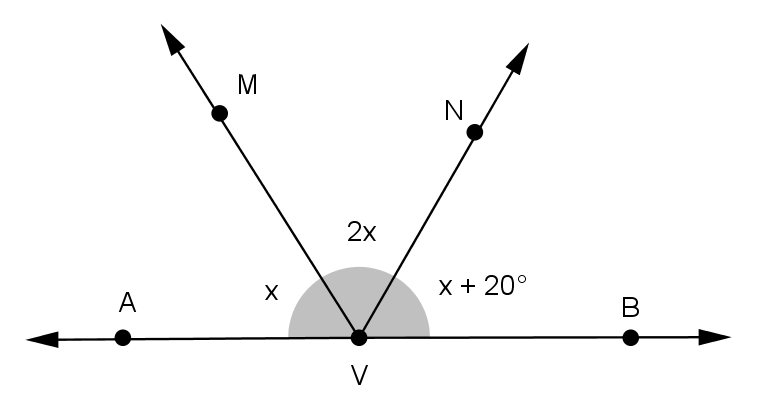
XÂM + MÂN + NÂY = XÂY ⇔ x + 2x + x + 20º = 180º ⇔ 4x = 180º - 20º ⇔ x = 160º/4 = 40º
Portanto:
XÂM = 40º
MÂN = 2 (40º) = 80º
NÂY = (40º) + 20º = 60º
Quatro ângulos â, ê, ô e û, unidos pelo mesmo vértice, formam um ângulo de volta completa. Determine os ângulos ô e û, sabendo que â e ê são retos e ô é o triplo de û.
De acordo com o enunciado:
Substituindo (II) e (III) em (I), vem:
â + ê + ô + û = 360º
90º + 90º + 3û + û = 360º
180º + 4û = 360º
4û = 360º - 180º ⇔ û = 180º/4 = 45º
Substituindo û = 45º em (III), vem:
ô = 3û ⇔ ô = 3 (45º) = 135º
A soma de dois ângulos adjacentes é 120º. Calcule a medida de cada ângulo, sabendo que a medida de um deles é o triplo do outro menos 40º.
Sejam x e y dois ângulos adjacentes. Tem-se:
Substituindo (II) em (I) vem:
x + y = 120º
(3y – 40º) + y = 120º
4y = 160º ⇔ y = 40º
Substituindo y = 40º em (II) vem:
x = 3y – 40º
x = 3(40º) – 40º
x = 120º - 40º ⇔ x = 80º
Esta foi uma demonstração gratuita.
Logue para ter acesso a todo conteúdo interativo.
Hum, ainda não criou conta!?
Crie sua conta e ative-a para ter acesso a todo conteúdo interativo.