Conjuntos estão presentes em nossas vidas e nem percebemos. Quer ver?

Pense em uma banda de música. Agora pense em um time de futebol.

Todos eles representam conjuntos.

• A banda de música é um conjunto composto por músicos.
• O time de futebol é um conjunto de jogadores.

Entendi

Conjunto é sinônimo de agrupamento, classe, coleção etc.

Exemplos:

• a) O conjunto dos campeões brasileiros da era dos pontos corridos é formado por: Cruzeiro, Santos, Corinthians, São Paulo, Flamengo, Fluminense, Atlético/MG e Palmeiras.
• b) O conjunto das vogais é composto pelas letras: a, e, i, o e u.

Voltar Entendi

Elementos do conjunto: São os objetos que constituem o conjunto.

Exemplos:

• a) Os elementos do conjunto dos campeões brasileiros da era dos pontos corridos são: Cruzeiro, Santos, Corinthians, São Paulo, Flamengo, Fluminense e Palmeiras.
• b) Os elementos do conjunto das vogais são as letras: a, e, i, o e u.

Voltar Entendi

Pertinência: Se um elemento é constituinte de um conjunto significa que ele pertence ao conjunto.

Os símbolo utilizados para relacionar elementos e conjuntos são ∈ (pertence) e ∉ (não-pertence).

Exemplos:

Chamando o conjunto dos campeões brasileiros da era dos pontos corridos de B, tem-se:

• a) Palmeiras ∈ B
• b) Sport ∉ B
• c) Fluminense ∈ B
• d) Vasco ∉ B

Chamando o conjunto das vogais de V, tem-se:

• a) a ∈ V
• b) b ∉ V
• c) c ∉ V
• d) u ∈ V

Voltar Entendi

Geralmente, os conjuntos são representados por letras maiúsculas e os elementos por letras minúsculas.

Os conjuntos podem ser representados por enumeração, propriedade e diagrama.

Enumeração

Enumera-se seus elementos entre { }.

Exemplos:

• a) O conjunto dos campeões brasileiros da era dos pontos corridos é {Cruzeiro, Santos, Corinthians, São Paulo, Flamengo, Fluminense, Palmeiras}.
• b) O conjunto das vogais é { a, e, i, o, u}.
• c) O conjunto dos números pares positivos menores que 8 é {2, 4, 6}.
• d) O conjunto dos números inteiros ímpares maiores que 3 e menores que 11 é {5, 7, 9}.

Propriedade

Representa o conjunto por meio de uma regra em que todos os elementos de um conjunto a satisfazem.

Exemplo:

Representando por propriedade o conjunto dos números inteiros ímpares maiores que 3 e menores que 11, tem-se:

A = {x | x é ímpar e 3 < x < 11}

Repare que A = {x | x é ímpar e 3 < x < 11} é o conjunto {5, 7, 9}.

Diagrama

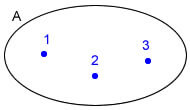
Representa o conjunto por meio de uma visualização geométrica, conhecida como diagrama de Venn.

Exemplo: A = {1, 2, 3}

Para exemplificar as três maneiras de representação de um conjunto, considere que o conjunto A seja formado pelos números inteiros positivos menores do que 4. Assim, tem-se:

Enumeração	Propriedade	Diagrama
{1, 2, 3}	{x ∈ \( \mathbb{N} \) | 0 < x < 4}

Voltar Entendi

Conjunto vazio (∅): É todo conjunto que não possui elemento algum.

Exemplos:

• a) O conjunto dos meses do ano que começam pela letra w, na língua portuguesa, é vazio.
• b) O conjunto dos números pares maiores que 2 e menores que 4 é vazio.

O conjunto vazio é indicado por ∅ ou { }.

Voltar Entendi

Conjunto unitário: É todo conjunto que possui apenas um elemento.

Exemplos:

• a) O conjunto dos números pares maiores que 2 e menores que 6 é {4}.
• b) O conjunto dos times mineiros campeões da era dos pontos corridos é {Cruzeiro}.

Voltar Entendi

Conjunto universo (U): É o conjunto que contém todos os conjuntos envolvidos no estudo.

Voltar Entendi

Conjunto finito: É o conjunto cuja quantidade de elementos é finita.

Exemplos:

• a) O conjunto A = {5, 3} tem dois elementos.
• b) O conjunto T = {a, b, c, d} tem quatro elementos.

Conjunto infinito: É o conjunto cuja quantidade de elementos não pode ser definida, ou seja, é infinita.

Exemplos:

• a) O conjunto A = {x | x é ímpar e x > 1}. Não é possível definir a quantidade de elementos pois há infinitos números ímpares que são maiores do que 1. Repare que A pode ser representado como A = {3, 5, 7, 9, 11, …}.
• b) O conjunto dos números pares maiores que 6 = {8, 10, 12, 14, ...}

Voltar Entendi

Complete o quadro abaixo.

Corrigir

Igualdade de conjuntos: Dois conjuntos A e B são iguais se e só se possuem os mesmos elementos.

Atenção:

• Não importa a ordem: {a, b, c} = {b, a, c}, por exemplo.
• Não importa a quantidade de elementos repetidos: {a, b, b, c, c, c, c} = {a, b, c}.

Voltar Entendi